| Figure 5: A partial derivation tree that justifies shifting |
Menhir Reference Manual |
Menhir is a parser generator. It turns high-level grammar specifications, decorated with “semantic actions” (fragments of executable code), into parsers. It is based on Knuth’s LR(1) parser construction technique [16]. It is strongly inspired by its precursors: yacc [12], ML-Yacc [24], and ocamlyacc [19], but offers a large number of minor and major improvements that make it a more modern tool.
This brief reference manual explains how to use Menhir. It does not attempt to explain context-free grammars, parsing, or the LR technique. Readers who have never used a parser generator are encouraged to read about these ideas first [1,2,9]. They are also invited to have a look at the demos directory in Menhir’s distribution.
Menhir currently offers a choice between several “back-ends”:
Potential users of Menhir should be warned that Menhir’s feature set is not completely stable. There is a tension between preserving a measure of compatibility with ocamlyacc, on the one hand, and introducing new ideas, on the other hand. Some aspects of the tool are potentially subject to incompatible changes. For instance, the “traditional” error-handling mechanism (which is based on the error token, see §10) is now regarded as deprecated and is likely to be entirely removed in the future.
Menhir is invoked as follows:
menhir option …option filename …filename
Each of the file names must end with .mly (unless --coq is used, in which case it must end with .vy) and denotes a partial grammar specification. These partial grammar specifications are joined (§5.1) to form a single, self-contained grammar specification, which is then processed. The following optional command line switches allow controlling many aspects of the process.
--base basename. This switch controls the base name of the .ml and .mli files that are produced. That is, the tool will produce files named basename.ml and basename.mli. Note that basename can contain occurrences of the / character, so it really specifies a path and a base name. When only one filename is provided on the command line, the default basename is obtained by depriving filename of its final .mly suffix. When multiple file names are provided on the command line, no default base name exists, so that the --base switch must be used.
--cmly. This switch causes Menhir to produce a .cmly file in addition to its normal operation. This file contains a (binary-form) representation of the grammar and automaton (see §13.1).
--comment. This switch causes a few comments to be inserted into the OCaml code that is written to the .ml file.
--compare-errors filename1 --compare-errors filename2. Two such switches must always be used in conjunction so as to specify the names of two .messages files, filename1 and filename2. Each file is read and internally translated to a mapping of states to messages. Menhir then checks that the left-hand mapping is a subset of the right-hand mapping. This feature is typically used in conjunction with --list-errors to check that filename2 is complete (that is, covers all states where an error can occur). For more information, see §11.
--compile-errors filename. This switch causes Menhir to read the file filename, which must obey the .messages file format, and to compile it to an OCaml function that maps a state number to a message. The OCaml code is sent to the standard output channel. At the same time, Menhir checks that the collection of input sentences in the file filename is correct and irredundant. For more information, see §11.
--coq. This switch causes Menhir to produce Coq code. See §12.
--coq-lib-no-path. This switch indicates that references to the Coq library MenhirLib should not be qualified. This was the default behavior of Menhir prior to 2018/05/30. This switch is provided for compatibility, but normally should not be used.
--coq-lib-path path. This switch allows specifying under what name (or path) the Coq support library is known to Coq. When Menhir runs in --coq mode, the generated parser contains references to several modules in this library. This path is used to qualify these references. Its default value is MenhirLib.
--coq-no-actions. (Used in conjunction with --coq.) This switch
causes the semantic actions present in the .vy file to be ignored and
replaced with tt, the unique inhabitant of Coq’s unit type. This
feature can be used to test the Coq back-end with a standard grammar, that is, a
grammar that contains OCaml semantic actions. Just rename the file from
.mly to .vy and set this switch.
--coq-no-complete. (Used in conjunction with --coq.) This switch disables the generation of the proof of completeness of the parser (§12). This can be necessary because the proof of completeness is possible only if the grammar has no conflict (not even a benign one, in the sense of §6.1). This can be desirable also because, for a complex grammar, completeness may require a heavy certificate and its validation by Coq may take time.
--coq-no-version-check. (Used in conjunction with --coq.) This switch prevents the generation of the check that verifies that the versions of Menhir and MenhirLib match.
--depend. See §14.
--dump. This switch causes a description of the automaton to be written to the file basename.automaton. This description is written after benign conflicts have been resolved, before severe conflicts are resolved (§6), and before extra reductions are introduced (§4.1.8).
--dump-menhirLib directory. This command causes Menhir to write the source code of the runtime library MenhirLib in the directory directory, and exit. The directory directory must exist already. Two files, named menhirLib.ml and menhirLib.mli, are created in it. This command can be useful to users with special needs who wish to use MenhirLib but do not want to rely on it being installed somewhere in the file system.
--dump-resolved. This command line switch causes a description of the automaton to be written to the file basename.automaton.resolved. This description is written after all conflicts have been resolved (§6) and after extra reductions have been introduced (§4.1.8).
--echo-errors filename. This switch causes Menhir to read the .messages file filename and to produce on the standard output channel just the input sentences. (That is, all messages, blank lines, and comments are filtered out.) For more information, see §11.
--echo-errors-concrete filename. This switch causes Menhir to
read the .messages file filename and to produce on the standard output
channel just the input sentences. Each sentence is followed with a comment of
the form ## Concrete syntax: ... that shows this sentence in concrete
syntax. This comment is printed only if the user has defined an alias for
every token (§4.1.3).
--exn-carries-state. This switch causes the exception Error to carry an integer parameter, as follows: exception Error of int. When the parser detects a syntax error, the number of the current state is reported in this way. This allows the caller to select a suitable syntax error message, along the lines described in §11. This switch is currently supported by the code back-end only. Thus, it is incompatible with --table. It is also incompatible with --fixed-exception.
--explain. This switch causes conflict explanations to be written to the file basename.conflicts. See also §6.
--external-tokens T. This switch causes the definition of the token type to be omitted in basename.ml and basename.mli. Instead, the generated parser relies on the type T.token, where T is an OCaml module name. It is up to the user to define module T and to make sure that it exports a suitable token type. Module T can be hand-written. It can also be automatically generated out of a grammar specification using the --only-tokens switch.
--fixed-exception. This switch causes the exception Error to be internally defined as a synonym for Parsing.Parse_error. This means that an exception handler that catches Parsing.Parse_error will also catch the generated parser’s Error. This helps increase Menhir’s compatibility with ocamlyacc. There is otherwise no reason to use this switch.
--infer, --infer-write-query, --infer-read-reply. See §14.
--inspection. This switch requires --table. It causes Menhir to generate not only the monolithic and incremental APIs (§9.1, §9.2), but also the inspection API (§9.3). Activating this switch causes a few more tables to be produced, resulting in somewhat larger code size.
--interpret. This switch causes Menhir to act as an interpreter, rather than as a compiler. No OCaml code is generated. Instead, Menhir reads sentences off the standard input channel, parses them, and displays outcomes. This switch can be usefully combined with --trace. For more information, see §8.
--interpret-error. This switch is analogous to --interpret, except Menhir expects every sentence to cause an error on its last token, and displays information about the state in which the error is detected, in the .messages file format. For more information, see §11.
--interpret-show-cst. This switch, used in conjunction with --interpret, causes Menhir to display a concrete syntax tree when a sentence is successfully parsed. For more information, see §8.
--list-errors. This switch causes Menhir to produce (on the standard output channel) a complete list of input sentences that cause an error, in the .messages file format. For more information, see §11.
--log-automaton level. When level is nonzero, this switch causes some information about the automaton to be logged to the standard error channel.
--log-code level. When level is nonzero, this switch causes some information about the generated OCaml code to be logged to the standard error channel.
--log-grammar level. When level is nonzero, this switch causes some information about the grammar to be logged to the standard error channel. When level is 2, the nullable, FIRST, and FOLLOW tables are displayed.
--merge-errors filename1 --merge-errors filename2. Two such switches must always be used in conjunction so as to specify the names of two .messages files, filename1 and filename2. This command causes Menhir to merge these two .messages files and print the result on the standard output channel. For more information, see §11.
--no-dollars. This switch disallows the use of positional keywords of the form $i.
--no-inline. This switch causes all %inline keywords in the grammar specification to be ignored. This is especially useful in order to understand whether these keywords help solve any conflicts.
--no-stdlib. This switch instructs Menhir to not use its standard library (§5.4).
--ocamlc command. See §14.
--ocamldep command. See §14.
--only-preprocess. This switch causes the grammar specifications to be transformed up to the point where the automaton’s construction can begin. The grammar specifications whose names are provided on the command line are joined (§5.1); all parameterized nonterminal symbols are expanded away (§5.2); type inference is performed, if --infer is enabled; all nonterminal symbols marked %inline are expanded away (§5.3). This yields a single, monolithic grammar specification, which is printed on the standard output channel.
--only-tokens. This switch causes the %token declarations in the grammar specification to be translated into a definition of the token type, which is written to the files basename.ml and basename.mli. No code is generated. This is useful when a single set of tokens is to be shared between several parsers. The directory demos/calc-two contains a demo that illustrates the use of this switch.
--random-seed seed. This switch allows the user to set a random seed. This seed influences the random sentence generator.
--random-self-init. This switch asks Menhir to choose a random seed in a nondeterministic (system-dependent) way. This seed influences the random sentence generator.
--random-sentence-length length. This switch allows the user to set a goal length for the random sentence generator. The generated sentences will normally have length at most length.
--random-sentence symbol. This switch asks Menhir to produce and display a random sentence that is generated by the nonterminal symbol symbol. The sentence is displayed as a sequence of terminal symbols, separated with spaces. Each terminal symbol is represented by its name.
The generated sentence is valid with respect to the grammar. If the grammar is in the class LR(1) (that is, if it has no conflicts at all), then the generated sentence is also accepted by the automaton. However, if the grammar has conflicts, then it may be the case that the sentence is rejected by the automaton.
The distribution of sentences is not uniform; some sentences (or fragments of sentences) may be more likely to appear than others.
The productions that involve the error pseudo-token are ignored by the random sentence generator.
--random-sentence-concrete symbol. This switch asks Menhir to produce and display a random sentence that is generated by the nonterminal symbol symbol. The sentence is displayed as a sequence of terminal symbols, separated with spaces. Each terminal symbol is represented by its token alias (§4.1.3). This assumes that a token alias has been defined for every token.
--raw-depend. See §14.
--reference-graph. This switch causes a description of the grammar’s dependency graph to be written to the file basename.dot. The graph’s vertices are the grammar’s nonterminal symbols. There is a directed edge from vertex A to vertex B if the definition of A refers to B. The file is in a format that is suitable for processing by the graphviz toolkit.
--require-aliases. This switch causes Menhir to check that a token alias (§4.1.3) has been defined for every token. There is no requirement for this alias to be actually used; it must simply exist. A missing alias gives rise to a warning (and, in --strict mode, to an error).
--stdlib directory. This switch exists only for backwards compatibility and is ignored. It may be removed in the future.
--strategy strategy. This switch selects an error-handling strategy, to be used by the code back-end, the table back-end, and the reference interpreter. The available strategies are legacy and simplified. (However, at the time of writing, the code back-end does not yet support the simplified strategy.) When this switch is omitted, the legacy strategy is used. The choice of a strategy matters only if the grammar uses the error token. For more details, see §10.
--strict. This switch causes several warnings about the grammar and about the automaton to be considered errors. This includes warnings about useless precedence declarations, non-terminal symbols that produce the empty language, unreachable non-terminal symbols, productions that are never reduced, conflicts that are not resolved by precedence declarations, end-of-stream conflicts, and missing token aliases.
--suggest-*. See §14.
--table. This switch causes Menhir to use the table back-end, as opposed to the code back-end, which is the default. When --table is used, Menhir produces significantly more compact and somewhat slower parsers. See §16 for a speed comparison.
The table back-end produces rather compact tables, which are analogous to those produced by yacc, bison, or ocamlyacc. These tables are not quite stand-alone: they are exploited by an interpreter, which is shipped as part of the support library MenhirLib. For this reason, when --table is used, MenhirLib must be made visible to the OCaml compilers, and must be linked into your executable program. The --suggest-* switches, described above, help do this.
The code back-end compiles the LR automaton directly into a nest of mutually recursive OCaml functions. In that case, MenhirLib is not required.
The incremental API (§9.2) and the inspection API (§9.3) are made available only by the table back-end.
--timings. This switch causes internal timing information to be sent to the standard error channel.
--timings-to filename. This switch causes internal timing information to be written to the file filename.
--trace. This switch causes tracing code to be inserted into the generated parser, so that, when the parser is run, its actions are logged to the standard error channel. This is analogous to ocamlrun’s p=1 parameter, except this switch must be enabled at compile time: one cannot selectively enable or disable tracing at runtime.
--unparsing. This switch requires --table. It causes Menhir to generate the unparsing API (§9.4). When this switch is enabled, the generated parser must be linked with the libraries menhirLib and menhirCST.
--unused-precedence-levels. This switch suppresses all warnings about useless %left, %right, %nonassoc and %prec declarations.
--unused-token symbol. This switch suppresses the warning that is normally emitted when Menhir finds that the terminal symbol symbol is unused.
--unused-tokens. This switch suppresses all of the warnings that are normally emitted when Menhir finds that some terminal symbols are unused.
--update-errors filename. This switch causes Menhir to read the .messages file filename and to produce on the standard output channel a new .messages file that is identical, except the auto-generated comments have been re-generated. For more information, see §11.
--version. This switch causes Menhir to print its own version number and exit.
A semicolon character (;) may appear after a declaration (§4.1).
An old-style rule (§4.2) may be terminated with a semicolon. Also, within an old-style rule, each producer (§4.2.3) may be terminated with a semicolon.
A new-style rule (§4.3) must not be terminated with a semicolon. Within such a rule, the elements of a sequence must be separated with semicolons.
Semicolons are not allowed to appear anywhere except in the places mentioned above. This is in contrast with ocamlyacc, which views semicolons as insignificant, just like whitespace.
Identifiers (id) coincide with OCaml identifiers, except they are not allowed to contain the quote (’) character. Following OCaml, identifiers that begin with a lowercase letter (lid) or with an uppercase letter (uid) are distinguished.
A quoted identifier qid is a string enclosed in double quotes. Such a string cannot contain a double quote or a backslash. Quoted identifiers are used as token aliases (§4.1.3).
Comments are C-style (surrounded with /* and */, cannot be nested), C++-style (announced by // and extending until the end of the line), or OCaml-style (surrounded with (* and *), can be nested). Of course, inside OCaml code, only OCaml-style comments are allowed.
OCaml type expressions are surrounded with < and >. Within such expressions, all references to type constructors (other than the built-in list, option, etc.) must be fully qualified.
specification ::= declaration … declaration %% rule … rule [ %% OCaml code ] declaration ::= %{ OCaml code %} %parameter < uid : OCaml module type > %token [ < OCaml type > ] uid [ qid ] … uid [ qid ] %nonassoc uid … uid %left uid … uid %right uid … uid %type < OCaml type > lid … lid %start [ < OCaml type > ] lid … lid %attribute actual … actual attribute … attribute % attribute %on_error_reduce lid … lid attribute ::= [@ name payload ] old syntax — rule ::= [ %public ] [ %inline ] lid [ ( id, …, id ) ] : [ | ] group | … | group group ::= production | … | production { OCaml code } [ %prec id ] production ::= producer … producer [ %prec id ] producer ::= [ lid = ] actual actual ::= id [ ( actual, …, actual ) ] actual ( ? ∣ +∣ * )group | … | group new syntax — rule ::= [ %public ] let lid [ ( id, …, id ) ] ( := ∣ == ) expression expression ::= [ | ] expression | … | expression [ pattern = ] expression ; expression id [ ( expression , …, expression ) ] expression ( ? ∣ +∣ * ){ OCaml code } [ %prec id ] < OCaml id > [ %prec id ] pattern ::= lid ∣ _ ∣ ∣ ( pattern , …, pattern )
Figure 1: Syntax of grammar specifications
The syntax of grammar specifications appears in Figure 1. The places where attributes can be attached are not shown; they are documented separately (§13.2). A grammar specification begins with a sequence of declarations (§4.1), ended by a mandatory %% keyword. Following this keyword, a sequence of rules is expected. Each rule defines a nonterminal symbol lid, whose name must begin with a lowercase letter. A rule is expressed either in the “old syntax” (§4.2) or in the “new syntax” (§4.3), which is slightly more elegant and powerful.
A header is a piece of OCaml code, surrounded with %{ and %}. It is copied verbatim at the beginning of the .ml file. It typically contains OCaml open directives and function definitions for use by the semantic actions. If a single grammar specification file contains multiple headers, their order is preserved. However, when two headers originate in distinct grammar specification files, the order in which they are copied to the .ml file is unspecified.
It is important to note that the header is copied by Menhir only to the .ml file, not to the .mli file. Therefore, it should not contain declarations that affect the meaning of the types that appear in the .mli file. Here are two problems that people commonly run into:
open Foo in
the header and declaring %type<t> bar, where the type t is
defined in the module Foo, will not work.
Solution: Write %type<Foo.t> bar.
module F = Foo
in the header can create a problem,
because it allows OCaml to infer that the symbol bar has type
F.t. Menhir relies on this information without realizing that
F is a local name, so in the end, the .mli file contains a reference
to F.t that does not make sense. The problem persists even if one
declares %type<Foo.t> bar, because Menhir prefers the type inferred
by OCaml over the type declared by the user.
Solution:
Wrap the module alias in an anonymous structure, like so:
open struct module F = Foo end.
(This requires OCaml 4.08 or newer.)
This makes the name F available in your code,
but forces OCaml to prefer the name Foo in the types that it infers.
A declaration of the form:
%parameter < uid : OCaml module type >
causes the entire parser to become parameterized over the OCaml module uid, that is, to become an OCaml functor. The directory demos/calc-param contains a demo that illustrates the use of this switch.
If a single specification file contains multiple %parameter declarations, their order is preserved, so that the module name uid introduced by one declaration is effectively in scope in the declarations that follow. When two %parameter declarations originate in distinct grammar specification files, the order in which they are processed is unspecified. Last, %parameter declarations take effect before %{ … %}, %token, %type, or %start declarations are considered, so that the module name uid introduced by a %parameter declaration is effectively in scope in all %{ … %}, %token, %type, or %start declarations, regardless of whether they precede or follow the %parameter declaration. This means, in particular, that the side effects of an OCaml header are observed only when the functor is applied, not when it is defined.
A declaration of the form:
%token [ < OCaml type > ] uid1 [ qid1 ] … uidn [ qidn ]
defines the identifiers uid1, …, uidn as tokens, that is, as terminal symbols in the grammar specification and as data constructors in the token type.
If an OCaml type t is present, then these tokens are considered to carry a semantic value of type t, otherwise they are considered to carry no semantic value.
If a quoted identifier qidi is present, then it is considered an alias for the terminal symbol uidi. (This feature, known as “token aliases”, is borrowed from Bison.) Throughout the grammar, the quoted identifier qidi is then synonymous with the identifier uidi. For example, if one declares:
%token PLUS "+"
then the quoted identifier "+" stands for the terminal symbol PLUS throughout the grammar. An example of the use of token aliases appears in the directory demos/calc-alias. Token aliases can be used to improve the readability of a grammar. One must keep in mind, however, that they are just syntactic sugar: they are not interpreted in any way by Menhir or conveyed to tools like ocamllex. They could be considered confusing by a reader who mistakenly believes that they are interpreted as string literals.
A declaration of one of the following forms:
%nonassoc uid1 … uidn
%left uid1 … uidn
%right uid1 … uidn
assigns both a priority level and an associativity status to the symbols uid1, …, uidn. The priority level assigned to uid1, …, uidn is not defined explicitly: instead, it is defined to be higher than the priority level assigned by the previous %nonassoc, %left, or %right declaration, and lower than that assigned by the next %nonassoc, %left, or %right declaration. The symbols uid1, …, uidn can be tokens (defined elsewhere by a %token declaration) or dummies (not defined anywhere). Both can be referred to as part of %prec annotations. Associativity status and priority levels allow shift/reduce conflicts to be silently resolved (§6).
A declaration of the form:
%type < OCaml type > lid1 … lidn
assigns an OCaml type to each of the nonterminal symbols lid1, …, lidn. For start symbols, providing an OCaml type is mandatory, but is usually done as part of the %start declaration. For other symbols, it is optional. Providing type information can improve the quality of OCaml’s type error messages.
A %type declaration may concern not only a nonterminal symbol, such as, say, expression, but also a fully applied parameterized nonterminal symbol, such as list(expression) or separated_list(COMMA, option(expression)).
The types provided as part of %type declarations are copied verbatim to the .ml and .mli files. In contrast, headers (§4.1.1) are copied to the .ml file only. For this reason, the types provided as part of %type declarations must make sense both in the presence and in the absence of these headers. They should typically be fully qualified types.
A declaration of the form:
%start [ < OCaml type > ] lid1 … lidn
declares the nonterminal symbols lid1, …, lidn to be start symbols. Each such symbol must be assigned an OCaml type either as part of the %start declaration or via separate %type declarations. Each of lid1, …, lidn becomes the name of a function whose signature is published in the .mli file and that can be used to invoke the parser.
Attribute declarations of the form %attribute actual … actual attribute … attribute and % attribute are explained in §13.2.
A declaration of the form:
%on_error_reduce lid1 … lidn
marks the nonterminal symbols lid1, …, lidn as potentially eligible for reduction when an invalid token is found. This may cause one or more extra reduction steps to be performed before the error is detected.
More precisely, this declaration affects the automaton as follows. Let us say that a production lid → … is “reducible on error” if its left-hand symbol lid appears in a %on_error_reduce declaration. After the automaton has been constructed and after any conflicts have been resolved, in every state s, the following algorithm is applied:
If step 3 above is executed in state s, then an error can never be detected in state s, since all error actions in state s are replaced with reduce actions. Error detection is deferred: at least one reduction takes place before the error is detected. It is a “spurious” reduction: in a canonical LR(1) automaton, it would not take place.
An %on_error_reduce declaration does not affect the language that is accepted by the automaton. It does not affect the location where an error is detected. It is used to control in which state an error is detected. If used wisely, it can make errors easier to report, because they are detected in a state for which it is easier to write an accurate diagnostic message (§11.3).
Like a %type declaration, an %on_error_reduce declaration may concern not only a nonterminal symbol, such as, say, expression, but also a fully applied parameterized nonterminal symbol, such as list(expression) or separated_list(COMMA, option(expression)).
The “on-error-reduce-priority” of a production is that of its left-hand symbol. The “on-error-reduce-priority” of a nonterminal symbol is determined implicitly by the order of %on_error_reduce declarations. In the declaration %on_error_reduce lid1 … lidn, the symbols lid1, …, lidn have the same “on-error-reduce-priority”. They have higher “on-error-reduce-priority” than the symbols listed in previous %on_error_reduce declarations, and lower “on-error-reduce-priority” than those listed in later %on_error_reduce declarations.
In its simplest form, a rule begins with the nonterminal symbol lid, followed by a colon character (:), and continues with a sequence of production groups (§4.2.1). Each production group is preceded with a vertical bar character (|); the very first bar is optional. The meaning of the bar is choice: the nonterminal symbol id develops to either of the production groups. We defer explanations of the keyword %public (§5.1), of the keyword %inline (§5.3), and of the optional formal parameters ( id, …, id ) (§5.2).
In its simplest form, a production group consists of a single production (§4.2.2), followed by an OCaml semantic action (§4.2.1) and an optional %prec annotation (§4.2.1). A production specifies a sequence of terminal and nonterminal symbols that should be recognized, and optionally binds identifiers to their semantic values.
A semantic action is a piece of OCaml code that is executed in order to assign a semantic value to the nonterminal symbol with which this production group is associated. A semantic action can refer to the (already computed) semantic values of the terminal or nonterminal symbols that appear in the production via the semantic value identifiers bound by the production.
For compatibility with ocamlyacc, semantic actions can also refer to unnamed semantic values via positional keywords of the form $1, $2, etc. This style is discouraged. (It is in fact forbidden if --no-dollars is turned on.) Furthermore, as a positional keyword of the form $i is internally rewritten as _i, the user should not use identifiers of the form _i.
An annotation of the form %prec id indicates that the precedence level of the production group is the level assigned to the symbol id via a previous %nonassoc, %left, or %right declaration (§4.1.4). In the absence of a %prec annotation, the precedence level assigned to each production is the level assigned to the rightmost terminal symbol that appears in it. It is undefined if the rightmost terminal symbol has an undefined precedence level or if the production mentions no terminal symbols at all. The precedence level assigned to a production is used when resolving shift/reduce conflicts (§6).
If multiple productions are present in a single group, then the semantic action and precedence annotation are shared between them. This short-hand effectively allows several productions to share a semantic action and precedence annotation without requiring textual duplication. It is legal only when every production binds exactly the same set of semantic value identifiers and when no positional semantic value keywords ($1, etc.) are used.
A production is a sequence of producers (§4.2.3), optionally followed by a %prec annotation (§4.2.1). If a precedence annotation is present, it applies to this production alone, not to other productions in the production group. It is illegal for a production and its production group to both carry %prec annotations.
A producer is an actual (§4.2.4), optionally preceded with a binding of a semantic value identifier, of the form lid =. The actual specifies which construction should be recognized and how a semantic value should be computed for that construction. The identifier lid, if present, becomes bound to that semantic value in the semantic action that follows. Otherwise, the semantic value can be referred to via a positional keyword ($1, etc.).
In its simplest form, an actual is just a terminal or nonterminal symbol id. If it is a parameterized non-terminal symbol (see §5.2), then it should be applied: id( actual, …, actual ) .
An actual may be followed with a modifier (?,
, or *). This is explained further on (see §5.2 and Figure 2).
An actual may also be an “anonymous rule”. In that case, one writes just the rule’s right-hand side, which takes the form group | … | group. (This form is allowed only as an argument in an application.) This form is expanded on the fly to a definition of a fresh non-terminal symbol, which is declared %inline. For instance, providing an anonymous rule as an argument to list:
list ( e = expression; SEMICOLON { e } )
is equivalent to writing this:
list ( expression_SEMICOLON )
where the non-terminal symbol expression_SEMICOLON is chosen fresh and is defined as follows:
%inline expression_SEMICOLON: | e = expression; SEMICOLON { e }
Please be warned that the new syntax is considered experimental and is subject to change in the future.
In its simplest form, a rule takes the form let lid := expression. Its left-hand side lid is a nonterminal symbol; its right-hand side is an expression. Such a rule defines an ordinary nonterminal symbol, while the alternate form let lid == expression defines an %inline nonterminal symbol (§5.3), that is, a macro. A rule can be preceded with the keyword %public (§5.1) and can be parameterized with a tuple of formal parameters ( id, …, id ) (§5.2). The various forms of expressions, listed in Figure 1, are:
The syntax of expressions, as presented in Figure 1, seems more permissive than it really is. In reality, a choice cannot be nested inside a sequence; a sequence cannot be nested in the left-hand side of a sequence; a semantic action cannot appear in the left-hand side of a sequence. (Thus, there is a stratification in three levels: choice expressions, sequence expressions, and atomic expressions, which corresponds roughly to the stratification of rules, productions, and producers in the old syntax.) Furthermore, an expression between parentheses ( expression ) is not a valid expression. To surround an expression with parentheses, one must write either midrule ( expression ) or endrule ( expression ) ; see §5.4 and Figure 3.
When a complex expression (e.g., a choice or a sequence) is placed in parentheses, as in id ( expression ), this is equivalent to using id ( s ) , where the fresh symbol s is declared as a synonym for this expression, via the declaration let s == expression. This idiom is also known as an anonymous rule (§4.2.4).
As an example of a rule in the new syntax, the parameterized nonterminal symbol option, which is part of Menhir’s standard library (§5.4), can be defined as follows:
let option(x) := | x = x ; { None } | x = x ; { Some x }
Using a pun, it can also be written as follows:
let option(x) := | = x ; { None }| = x ; { Some x }
Using a pun and a point-free semantic action, it can also be expressed as follows:
let option(x) := | = x ; { None }| = x ; < Some >
As another example, the parameterized symbol delimited, also part of Menhir’s standard library (§5.4), can be defined in the new syntax as follows:
let delimited(opening, x, closing) == opening ; = x ; closing ; <>
The use of == indicates that this is a macro, i.e., an %inline nonterminal symbol (see §5.3). The identity semantic action <> is here synonymous with { x }.
Other illustrations of the new syntax can be found in the directories demos/calc-new-syntax and demos/calc-ast.
Grammar specifications can be split over multiple files. When Menhir is invoked with multiple argument file names, it considers each of these files as a partial grammar specification, and joins these partial specifications in order to obtain a single, complete specification.
This feature is intended to promote a form a modularity. It is hoped that, by splitting large grammar specifications into several “modules”, they can be made more manageable. It is also hoped that this mechanism, in conjunction with parameterization (§5.2), will promote sharing and reuse. It should be noted, however, that this is only a weak form of modularity. Indeed, partial specifications cannot be independently processed (say, checked for conflicts). It is necessary to first join them, so as to form a complete grammar specification, before any kind of grammar analysis can be done.
This mechanism is, in fact, how Menhir’s standard library (§5.4) is made available: even though its name does not appear on the command line, it is automatically joined with the user’s explicitly-provided grammar specifications, making the standard library’s definitions globally visible.
A partial grammar specification, or module, contains declarations and rules, just like a complete one: there is no visible difference. Of course, it can consist of only declarations, or only rules, if the user so chooses. (Don’t forget the mandatory %% keyword that separates declarations and rules. It must be present, even if one of the two sections is empty.)
It should be noted that joining is not a purely textual process. If two modules happen to define a nonterminal symbol by the same name, then it is considered, by default, that this is an accidental name clash. In that case, each of the two nonterminal symbols is silently renamed so as to avoid the clash. In other words, by default, a nonterminal symbol defined in module A is considered private, and cannot be defined again, or referred to, in module B.
Naturally, it is sometimes desirable to define a nonterminal symbol N in module A and to refer to it in module B. This is permitted if N is public, that is, if either its definition carries the keyword %public or N is declared to be a start symbol. A public nonterminal symbol is never renamed, so it can be referred to by modules other than its defining module.
In fact, it is permitted to split the definition of a public nonterminal symbol, over multiple modules and/or within a single module. That is, a public nonterminal symbol N can have multiple definitions, within one module and/or in distinct modules. All of these definitions are joined using the choice (|) operator. For instance, in the grammar of a programming language, the definition of the nonterminal symbol expression could be split into multiple modules, where one module groups the expression forms that have to do with arithmetic, one module groups those that concern function definitions and function calls, one module groups those that concern object definitions and method calls, and so on.
Another use of modularity consists in placing all %token declarations in one module, and the actual grammar specification in another module. The module that contains the token definitions can then be shared, making it easier to define multiple parsers that accept the same type of tokens. (On this topic, see demos/calc-two.)
A rule (that is, the definition of a nonterminal symbol) can be parameterized over an arbitrary number of symbols, which are referred to as formal parameters.
For instance, here is the definition of the parameterized nonterminal symbol option, taken from the standard library (§5.4):
%public option(X): | { None } | x = X { Some x }
This definition states that option(X) expands to either the empty string, producing the semantic value None, or to the string X, producing the semantic value Some x, where x is the semantic value of X. In this definition, the symbol X is abstract: it stands for an arbitrary terminal or nonterminal symbol. The definition is made public, so option can be referred to within client modules.
A client who wishes to use option simply refers to it, together with an actual parameter – a symbol that is intended to replace X. For instance, here is how one might define a sequence of declarations, preceded with optional commas:
declarations: | { [] } | ds = declarations; option(COMMA); d = declaration { d :: ds }
This definition states that declarations expands either to the empty string or to declarations followed by an optional comma followed by declaration. (Here, COMMA is presumably a terminal symbol.) When this rule is encountered, the definition of option is instantiated: that is, a copy of the definition, where COMMA replaces X, is produced. Things behave exactly as if one had written:
optional_comma: | { None } | x = COMMA { Some x } declarations: | { [] } | ds = declarations; optional_comma; d = declaration { d :: ds }
Note that, even though COMMA presumably has been declared as a token with no semantic value, writing x = COMMA is legal, and binds x to the unit value. This design choice ensures that the definition of option makes sense regardless of the nature of X: that is, X can be instantiated with a terminal symbol, with or without a semantic value, or with a nonterminal symbol.
In general, the definition of a nonterminal symbol N can be parameterized with an arbitrary number of formal parameters. When N is referred to within a production, it must be applied to the same number of actuals. In general, an actual is:
For instance, here is a rule whose single production consists of a single producer, which contains several, nested actuals. (This example is discussed again in §5.4.)
plist(X): | xs = loption(delimited(LPAREN, separated_nonempty_list(COMMA, X), RPAREN)) { xs }
actual? is syntactic sugar for option(actual) actual +is syntactic sugar for nonempty_list(actual) actual* is syntactic sugar for list(actual)
Figure 2: Syntactic sugar for simulating regular expressions, also known as EBNF
Applications of the parameterized nonterminal symbols option, nonempty_list, and list, which are defined in the standard library (§5.4), can be written using a familiar, regular-expression like syntax (Figure 2).
A formal parameter can itself expect parameters. For instance, here is a rule that defines the syntax of procedures in an imaginary programming language:
procedure(list): | PROCEDURE ID list(formal) SEMICOLON block SEMICOLON { … }
This rule states that the token ID, which represents the name of the procedure, should be followed with a list of formal parameters. (The definitions of the nonterminal symbols formal and block are not shown.) However, because list is a formal parameter, as opposed to a concrete nonterminal symbol defined elsewhere, this definition does not specify how the list is laid out: which token, if any, is used to separate, or terminate, list elements? is the list allowed to be empty? and so on. A more concrete notion of procedure is obtained by instantiating the formal parameter list: for instance, procedure(plist), where plist is the parameterized nonterminal symbol defined earlier, is a valid application.
Definitions and uses of parameterized nonterminal symbols are checked for consistency before they are expanded away. In short, it is checked that, wherever a nonterminal symbol is used, it is supplied with actual arguments in appropriate number and of appropriate nature. This guarantees that expansion of parameterized definitions terminates and produces a well-formed grammar as its outcome.
It is well-known that the following grammar of arithmetic expressions does not work as expected: that is, in spite of the priority declarations, it has shift/reduce conflicts.
%token < int > INT %token PLUS TIMES %left PLUS %left TIMES %% expression: | i = INT { i } | e = expression; o = op; f = expression { o e f } op: | PLUS { ( + ) } | TIMES { ( * ) }
The trouble is, the precedence level of the production expression → expression op expression is undefined, and there is no sensible way of defining it via a %prec declaration, since the desired level really depends upon the symbol that was recognized by op: was it PLUS or TIMES?
The standard workaround is to abandon the definition of op as a separate nonterminal symbol, and to inline its definition into the definition of expression, like this:
expression: | i = INT { i } | e = expression; PLUS; f = expression { e + f } | e = expression; TIMES; f = expression { e * f }
This avoids the shift/reduce conflict, but gives up some of the original specification’s structure, which, in realistic situations, can be damageable. Fortunately, Menhir offers a way of avoiding the conflict without manually transforming the grammar, by declaring that the nonterminal symbol op should be inlined:
expression: | i = INT { i } | e = expression; o = op; f = expression { o e f } %inline op: | PLUS { ( + ) } | TIMES { ( * ) }
The %inline keyword causes all references to op to be replaced with its definition. In this example, the definition of op involves two productions, one that develops to PLUS and one that expands to TIMES, so every production that refers to op is effectively turned into two productions, one that refers to PLUS and one that refers to TIMES. After inlining, op disappears and expression has three productions: that is, the result of inlining is exactly the manual workaround shown above.
In some situations, inlining can also help recover a slight efficiency margin. For instance, the definition:
%inline plist(X): | xs = loption(delimited(LPAREN, separated_nonempty_list(COMMA, X), RPAREN)) { xs }
effectively makes plist(X) an alias for the right-hand side loption(…). Without the %inline keyword, the language recognized by the grammar would be the same, but the LR automaton would probably have one more state and would perform one more reduction at run time.
The %inline keyword does not affect the computation of positions (§7). The same positions are computed, regardless of where %inline keywords are placed.
If the semantic actions have side effects, the %inline keyword can affect the order in which these side effects take place. In the example of op and expression above, if for some reason the semantic action associated with op has a side effect (such as updating a global variable, or printing a message), then, by inlining op, we delay this side effect, which takes place after the second operand has been recognized, whereas in the absence of inlining it takes place as soon as the operator has been recognized.
Name Recognizes Produces Comment endrule(X) X α, if X : α (inlined) midrule(X) X α, if X : α option(X) є | X α option, if X : α (also X?) ioption(X) є | X α option, if X : α (inlined) boption(X) є | X bool loption(X) є | X α list, if X : α list pair(X, Y) X Y α×β, if X : α and Y : β separated_pair(X, sep, Y) X sep Y α×β, if X : α and Y : β preceded(opening, X) opening X α, if X : α terminated(X, closing) X closing α, if X : α delimited(opening, X, closing) opening X closing α, if X : α list(X) a possibly empty sequence of X’s α list, if X : α (also X*) nonempty_list(X) a nonempty sequence of X’s α list, if X : α (also X +)separated_list(sep, X) a possibly empty sequence of X’s separated with sep’s α list, if X : α separated_nonempty_list(sep, X) a nonempty sequence of X’s separated with sep’s α list, if X : α rev(X) X α list, if X : α list (inlined) flatten(X) X α list, if X : α list list (inlined) append(X, Y) X Y α list, if X, Y : α list (inlined)
Figure 3: Summary of the standard library; see standard.mly for details
Once equipped with a rudimentary module system (§5.1), parameterization (§5.2), and inlining (§5.3), it is straightforward to propose a collection of commonly used definitions, such as options, sequences, lists, and so on. This standard library is joined, by default, with every grammar specification. A summary of the nonterminal symbols offered by the standard library appears in Figure 3. See also the short-hands documented in Figure 2.
By relying on the standard library, a client module can concisely define more elaborate notions. For instance, the following rule:
%inline plist(X): | xs = loption(delimited(LPAREN, separated_nonempty_list(COMMA, X), RPAREN)) { xs }
causes plist(X) to recognize a list of X’s, where the empty list is represented by the empty string, and a non-empty list is delimited with parentheses and comma-separated.
The standard library is stored in a file named standard.mly, which is embedded inside Menhir when it is built. The command line switch --no-stdlib instructs Menhir to not load the standard library.
The meaning of the symbols defined in the standard library (Figure 3) should be clear in most cases. Yet, the symbols endrule(X) and midrule(X) deserve an explanation. Both take an argument X, which typically will be instantiated with an anonymous rule (§4.2.4). Both are defined as a synonym for X. In both cases, this allows placing an anonymous subrule in the middle of a rule.
For instance, the following is a well-formed production:
|
This production consists of three producers, namely cat and endrule(dog { OCaml code1 }) and cow, and a semantic action { OCaml code2 }. Because endrule(X) is declared as an %inline synonym for X, the expansion of anonymous rules (§4.2.4), followed with the expansion of %inline symbols (§5.3), transforms the above production into the following:
|
Note that OCaml code1 moves to the end of the rule, which means that this code is executed only after cat, dog and cow have been recognized. In this example, the use of endrule is rather pointless, as the expanded code is more concise and clearer than the original code. Still, endrule can be useful when its actual argument is an anonymous rule with multiple branches.
midrule is used in exactly the same way as endrule, but its expansion is different. For instance, the following is a well-formed production:
|
(There is no dog in this example; this is intentional.) Because midrule(X) is a synonym for X, but is not declared %inline, the expansion of anonymous rules (§4.2.4), followed with the expansion of %inline symbols (§5.3), transforms the above production into the following:
|
where the fresh nonterminal symbol xxx is separately defined by the rule xxx: { OCaml code1 } . Thus, xxx recognizes the empty string, and as soon as it is recognized, OCaml code1 is executed. This is known as a “mid-rule action”.
When a shift/reduce or reduce/reduce conflict is detected, it is classified as either benign, if it can be resolved by consulting user-supplied precedence declarations, or severe, if it cannot. Benign conflicts are not reported. Severe conflicts are reported and, if the --explain switch is on, explained.
A shift/reduce conflict involves a single token (the one that one might wish to shift) and one or more productions (those that one might wish to reduce). When such a conflict is detected, the precedence level (§4.1.4, §4.2.1) of these entities are looked up and compared as follows:
In either of these cases, the conflict is considered benign. Otherwise, it is considered severe. Note that a reduce/reduce conflict is always considered severe, unless it happens to be subsumed by a benign multi-way shift/reduce conflict (item 3 above).
When the --dump switch is on, a description of the automaton is written to the .automaton file. Severe conflicts are shown as part of this description. Fortunately, there is also a way of understanding conflicts in terms of the grammar, rather than in terms of the automaton. When the --explain switch is on, a textual explanation is written to the .conflicts file.
Not all conflicts are explained in this file: instead, only one conflict per automaton state is explained. This is done partly in the interest of brevity, but also because Pager’s algorithm can create artificial conflicts in a state that already contains a true LR(1) conflict; thus, one cannot hope in general to explain all of the conflicts that appear in the automaton. As a result of this policy, once all conflicts explained in the .conflicts file have been fixed, one might need to run Menhir again to produce yet more conflict explanations.
%token IF THEN ELSE %start < expression > expression %% expression: | … | IF b = expression THEN e = expression { … } | IF b = expression THEN e = expression ELSE f = expression { … } | …
Figure 4: Basic example of a shift/reduce conflict
Figure 4 shows a grammar specification with a typical shift/reduce conflict. When this specification is analyzed, the conflict is detected, and an explanation is written to the .conflicts file. The explanation first indicates in which state the conflict lies by showing how that state is reached. Here, it is reached after recognizing the following string of terminal and nonterminal symbols—the conflict string:
IF expression THEN IF expression THEN expression
Allowing the conflict string to contain both nonterminal and terminal symbols usually makes it shorter and more readable. If desired, a conflict string composed purely of terminal symbols could be obtained by replacing each occurrence of a nonterminal symbol N with an arbitrary N-sentence.
The conflict string can be thought of as a path that leads from one of the automaton’s start states to the conflict state. When multiple such paths exist, the one that is displayed is chosen shortest. Nevertheless, it may sometimes be quite long. In that case, artificially (and temporarily) declaring some existing nonterminal symbols to be start symbols has the effect of adding new start states to the automaton and can help produce shorter conflict strings. Here, expression was declared to be a start symbol, which is why the conflict string is quite short.
In addition to the conflict string, the .conflicts file also states that the conflict token is ELSE. That is, when the automaton has recognized the conflict string and when the lookahead token (the next token on the input stream) is ELSE, a conflict arises. A conflict corresponds to a choice: the automaton is faced with several possible actions, and does not know which one should be taken. This indicates that the grammar is not LR(1). The grammar may or may not be inherently ambiguous.
In our example, the conflict string and the conflict token are enough to understand why there is a conflict: when two IF constructs are nested, it is ambiguous which of the two constructs the ELSE branch should be associated with. Nevertheless, the .conflicts file provides further information: it explicitly shows that there exists a conflict, by proving that two distinct actions are possible. Here, one of these actions consists in shifting, while the other consists in reducing: this is a shift/reduce conflict.
A proof takes the form of a partial derivation tree whose fringe begins with the conflict string, followed by the conflict token. A derivation tree is a tree whose nodes are labeled with symbols. The root node carries a start symbol. A node that carries a terminal symbol is considered a leaf, and has no children. A node that carries a nonterminal symbol N either is considered a leaf, and has no children; or is not considered a leaf, and has n children, where n≥ 0, labeled x1,…,xn, where N → x1,…,xn is a production. The fringe of a partial derivation tree is the string of terminal and nonterminal symbols carried by the tree’s leaves. A string of terminal and nonterminal symbols that is the fringe of some partial derivation tree is a sentential form.

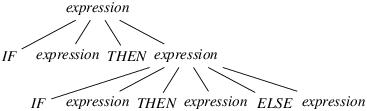
Figure 5: A partial derivation tree that justifies shifting
expression IF expression THEN expression IF expression THEN expression . ELSE expression
Figure 6: A textual version of the tree in Figure 5
In our example, the proof that shifting is possible is the derivation tree shown in Figures 5 and 6. At the root of the tree is the grammar’s start symbol, expression. This symbol develops into the string IF expression THEN expression, which forms the tree’s second level. The second occurrence of expression in that string develops into IF expression THEN expression ELSE expression, which forms the tree’s last level. The tree’s fringe, a sentential form, is the string IF expression THEN IF expression THEN expression ELSE expression. As announced earlier, it begins with the conflict string IF expression THEN IF expression THEN expression, followed with the conflict token ELSE.
In Figure 6, the end of the conflict string is materialized with a dot. Note that this dot does not occupy the rightmost position in the tree’s last level. In other words, the conflict token (ELSE) itself occurs on the tree’s last level. In practical terms, this means that, after the automaton has recognized the conflict string and peeked at the conflict token, it makes sense for it to shift that token.
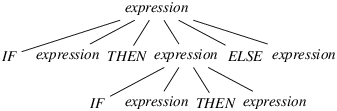
Figure 7: A partial derivation tree that justifies reducing
expression IF expression THEN expression ELSE expression // lookahead token appears IF expression THEN expression .
Figure 8: A textual version of the tree in Figure 7
In our example, the proof that reducing is possible is the derivation tree shown in Figures 7 and 8. Again, the sentential form found at the fringe of the tree begins with the conflict string, followed with the conflict token.
Again, in Figure 8, the end of the conflict string is materialized with a dot. Note that, this time, the dot occupies the rightmost position in the tree’s last level. In other words, the conflict token (ELSE) appeared on an earlier level (here, on the second level). This fact is emphasized by the comment // lookahead token appears found at the second level. In practical terms, this means that, after the automaton has recognized the conflict string and peeked at the conflict token, it makes sense for it to reduce the production that corresponds to the tree’s last level—here, the production is expression → IF expression THEN expression.
Figures 9 and 10 show a partial derivation tree that justifies reduction in a more complex situation. (This derivation tree is relative to a grammar that is not shown.) Here, the conflict string is DATA UIDENT EQUALS UIDENT; the conflict token is LIDENT. It is quite clear that the fringe of the tree begins with the conflict string. However, in this case, the fringe does not explicitly exhibit the conflict token. Let us examine the tree more closely and answer the question: following UIDENT, what’s the next terminal symbol on the fringe?
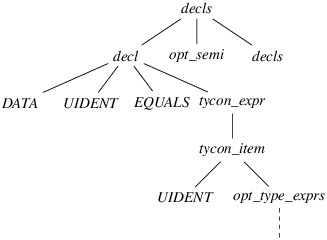
Figure 9: A partial derivation tree that justifies reducing
decls decl opt_semi decls // lookahead token appears because opt_semi can vanish and decls can begin with LIDENT DATA UIDENT EQUALS tycon_expr // lookahead token is inherited tycon_item // lookahead token is inherited UIDENT opt_type_exprs // lookahead token is inherited .
Figure 10: A textual version of the tree in Figure 9
First, note that opt_type_exprs is not a leaf node, even though it has no children. The grammar contains the production opt_type_exprs → є: the nonterminal symbol opt_type_exprs develops to the empty string. (This is made clear in Figure 10, where a single dot appears immediately below opt_type_exprs.) Thus, opt_type_exprs is not part of the fringe.
Next, note that opt_type_exprs is the rightmost symbol within its level. Thus, in order to find the next symbol on the fringe, we have to look up one level. This is the meaning of the comment // lookahead token is inherited. Similarly, tycon_item and tycon_expr appear rightmost within their level, so we again have to look further up.
This brings us back to the tree’s second level. There, decl is not the rightmost symbol: next to it, we find opt_semi and decls. Does this mean that opt_semi is the next symbol on the fringe? Yes and no. opt_semi is a nonterminal symbol, but we are really interested in finding out what the next terminal symbol on the fringe could be. The partial derivation tree shown in Figures 9 and 10 does not explicitly answer this question. In order to answer it, we need to know more about opt_semi and decls.
Here, opt_semi stands (as one might have guessed) for an optional semicolon, so the grammar contains a production opt_semi → є. This is indicated by the comment // opt_semi can vanish. (Nonterminal symbols that generate є are also said to be nullable.) Thus, one could choose to turn this partial derivation tree into a larger one by developing opt_semi into є, making it a non-leaf node. That would yield a new partial derivation tree where the next symbol on the fringe, following UIDENT, is decls.
Now, what about decls? Again, it is a nonterminal symbol, and we are really interested in finding out what the next terminal symbol on the fringe could be. Again, we need to imagine how this partial derivation tree could be turned into a larger one by developing decls. Here, the grammar happens to contain a production of the form decls → LIDENT … This is indicated by the comment // decls can begin with LIDENT. Thus, by developing decls, it is possible to construct a partial derivation tree where the next symbol on the fringe, following UIDENT, is LIDENT. This is precisely the conflict token.
To sum up, there exists a partial derivation tree whose fringe begins with the conflict string, followed with the conflict token. Furthermore, in that derivation tree, the dot occupies the rightmost position in the last level. As in our previous example, this means that, after the automaton has recognized the conflict string and peeked at the conflict token, it makes sense for it to reduce the production that corresponds to the tree’s last level—here, the production is opt_type_exprs → є.
Understanding conflicts requires comparing two (or more) derivation trees. It is frequent for these trees to exhibit a common factor, that is, to exhibit identical structure near the top of the tree, and to differ only below a specific node. Manual identification of that node can be tedious, so Menhir performs this work automatically. When explaining a n-way conflict, it first displays the greatest common factor of the n derivation trees. A question mark symbol (?) is used to identify the node where the trees begin to differ. Then, Menhir displays each of the n derivation trees, without their common factor – that is, it displays n sub-trees that actually begin to differ at the root. This should make visual comparisons significantly easier.
It is unspecified how severe conflicts are resolved. Menhir attempts to mimic ocamlyacc’s specification, that is, to resolve shift/reduce conflicts in favor of shifting, and to resolve reduce/reduce conflicts in favor of the production that textually appears earliest in the grammar specification. However, this specification is inconsistent in case of three-way conflicts, that is, conflicts that simultaneously involve a shift action and several reduction actions. Furthermore, textual precedence can be undefined when the grammar specification is split over multiple modules. In short, Menhir’s philosophy is that
so you should not care how they are resolved.
Menhir’s treatment of the end of the token stream is (believed to be) fully compatible with ocamlyacc’s. Yet, Menhir attempts to be more user-friendly by warning about a class of so-called “end-of-stream conflicts”.
In many textbooks on parsing, it is assumed that the lexical analyzer, which produces the token stream, produces a special token, written #, to signal that the end of the token stream has been reached. A parser generator can take advantage of this by transforming the grammar: for each start symbol S in the original grammar, a new start symbol S’ is defined, together with the production S′→ S# . The symbol S is no longer a start symbol in the new grammar. This means that the parser will accept a sentence derived from S only if it is immediately followed by the end of the token stream.
This approach has the advantage of simplicity. However, ocamlyacc and Menhir do not follow it, for several reasons. Perhaps the most convincing one is that it is not flexible enough: sometimes, it is desirable to recognize a sentence derived from S, without requiring that it be followed by the end of the token stream: this is the case, for instance, when reading commands, one by one, on the standard input channel. In that case, there is no end of stream: the token stream is conceptually infinite. Furthermore, after a command has been recognized, we do not wish to examine the next token, because doing so might cause the program to block, waiting for more input.
In short, ocamlyacc and Menhir’s approach is to recognize a sentence derived from S and to not look, if possible, at what follows. However, this is possible only if the definition of S is such that the end of an S-sentence is identifiable without knowledge of the lookahead token. When the definition of S does not satisfy this criterion, and end-of-stream conflict arises: after a potential S-sentence has been read, there can be a tension between consulting the next token, in order to determine whether the sentence is continued, and not consulting the next token, because the sentence might be over and whatever follows should not be read. Menhir warns about end-of-stream conflicts, whereas ocamlyacc does not.
Technically, Menhir proceeds as follows. A # symbol is introduced. It is, however, only a pseudo-token: it is never produced by the lexical analyzer. For each start symbol S in the original grammar, a new start symbol S’ is defined, together with the production S′→ S. The corresponding start state of the LR(1) automaton is composed of the LR(1) item S′ → . S [# ]. That is, the pseudo-token # initially appears in the lookahead set, indicating that we expect to be done after recognizing an S-sentence. During the construction of the LR(1) automaton, this lookahead set is inherited by other items, with the effect that, in the end, the automaton has:
A state of the automaton has a reduce action on # if, in that state, an S-sentence has been read, so that the job is potentially finished. A state has a shift or reduce action on a physical token if, in that state, more tokens potentially need to be read before an S-sentence is recognized. If a state has a reduce action on #, then that action should be taken without requesting the next token from the lexical analyzer. On the other hand, if a state has a shift or reduce action on a physical token, then the lookahead token must be consulted in order to determine if that action should be taken.
%token < int > INT %token PLUS TIMES %left PLUS %left TIMES %start < int > expr %% expr: | i = INT { i } | e1 = expr PLUS e2 = expr { e1 + e2 } | e1 = expr TIMES e2 = expr { e1 * e2 }
Figure 11: Basic example of an end-of-stream conflict
State 6: expr -> expr . PLUS expr [ # TIMES PLUS ] expr -> expr PLUS expr . [ # TIMES PLUS ] expr -> expr . TIMES expr [ # TIMES PLUS ] -- On TIMES shift to state 3 -- On # PLUS reduce production expr -> expr PLUS expr State 4: expr -> expr . PLUS expr [ # TIMES PLUS ] expr -> expr . TIMES expr [ # TIMES PLUS ] expr -> expr TIMES expr . [ # TIMES PLUS ] -- On # TIMES PLUS reduce production expr -> expr TIMES expr State 2: expr' -> expr . [ # ] expr -> expr . PLUS expr [ # TIMES PLUS ] expr -> expr . TIMES expr [ # TIMES PLUS ] -- On TIMES shift to state 3 -- On PLUS shift to state 5 -- On # accept expr
Figure 12: Part of an LR automaton for the grammar in Figure 11
… %token END %start < int > main // instead of expr %% main: | e = expr END { e } expr: | …
Figure 13: Fixing the grammar specification in Figure 11
An end-of-stream conflict arises when a state has distinct actions on # and on at least one physical token. In short, this means that the end of an S-sentence cannot be unambiguously identified without examining one extra token. Menhir’s default behavior, in that case, is to suppress the action on #, so that more input is always requested.
Figure 11 shows a grammar that has end-of-stream conflicts. When this grammar is processed, Menhir warns about these conflicts, and further warns that expr is never accepted. Let us explain.
Part of the corresponding automaton, as described in the .automaton file, is shown in Figure 12. Explanations at the end of the .automaton file (not shown) point out that states 6 and 2 have an end-of-stream conflict. Indeed, both states have distinct actions on # and on the physical token TIMES. It is interesting to note that, even though state 4 has actions on # and on physical tokens, it does not have an end-of-stream conflict. This is because the action taken in state 4 is always to reduce the production expr → expr TIMES expr, regardless of the lookahead token.
By default, Menhir produces a parser where end-of-stream conflicts are resolved in favor of looking ahead: that is, the problematic reduce actions on # are suppressed. This means, in particular, that the accept action in state 2, which corresponds to reducing the production expr → expr’, is suppressed. This explains why the symbol expr is never accepted: because expressions do not have an unambiguous end marker, the parser will always request one more token and will never stop.
In order to avoid this end-of-stream conflict, the standard solution is to introduce a new token, say END, and to use it as an end marker for expressions. The END token could be generated by the lexical analyzer when it encounters the actual end of stream, or it could correspond to a piece of concrete syntax, say, a line feed character, a semicolon, or an end keyword. The solution is shown in Figure 13.
When an ocamllex-generated lexical analyzer produces a token, it updates
two fields, named lex_start_p and lex_curr_p, in its environment
record, whose type is Lexing.lexbuf. Each of these fields holds a value
of type Lexing.position. Together, they represent the token’s start and
end positions within the text that is being scanned. These fields are read by
Menhir after calling the lexical analyzer, so it is the lexical
analyzer’s responsibility to correctly set these fields.
A position consists
mainly of an offset (the position’s pos_cnum field), but also holds
information about the current file name, the current line number, and the
current offset within the current line. (Not all ocamllex-generated analyzers
keep this extra information up to date. This must be explicitly programmed by
the author of the lexical analyzer.)
$startposstart position of the first symbol in the production’s right-hand side, if there is one; end position of the most recently parsed symbol, otherwise $endposend position of the last symbol in the production’s right-hand side, if there is one; end position of the most recently parsed symbol, otherwise $startpos($i | id)start position of the symbol named $i or id$endpos($i | id)end position of the symbol named $i or id$symbolstartpos start position of the leftmost symbol id such that $startpos(id)!=$endpos(id);if there is no such symbol, $endpos$startofs$endofs$startofs($i | id)same as above, but produce an integer offset instead of a position $endofs($i | id)$symbolstartofs$locstands for the pair ($startpos, $endpos)$loc(id)stands for the pair ($startpos(id), $endpos(id))$slocstands for the pair ($symbolstartpos, $endpos)
Figure 14: Position-related keywords
symbol_start_pos()$symbolstartpos symbol_end_pos()$endposrhs_start_pos i$startpos($i)(1 ≤ i ≤ n) rhs_end_pos i$endpos($i)(1 ≤ i ≤ n) symbol_start()$symbolstartofssymbol_end()$endofsrhs_start i$startofs($i)(1 ≤ i ≤ n) rhs_end i$endofs($i)(1 ≤ i ≤ n)
Figure 15: Translating position-related incantations from ocamlyacc to Menhir
This mechanism allows associating pairs of positions with terminal symbols. If desired, Menhir automatically extends it to nonterminal symbols as well. That is, it offers a mechanism for associating pairs of positions with terminal or nonterminal symbols. This is done by making a set of keywords available to semantic actions (Figure 14). These keywords are not available outside of a semantic action: in particular, they cannot be used within an OCaml header.
OCaml’s standard library module Parsing is deprecated. The functions that it offers can be called, but will return dummy positions.
We remark that, if the current production has an empty right-hand side, then
$startpos and $endpos are equal, and (by convention) are the end
position of the most recently parsed symbol (that is, the symbol that happens
to be on top of the automaton’s stack when this production is reduced). If
the current production has a nonempty right-hand side, then
$startpos is the same as $startpos($1) and
$endpos is the same as $endpos($n),
where n is the length of the right-hand side.
More generally, if the current production has matched a sentence of length
zero, then $startpos and $endpos will be equal, and conversely.
The position $startpos is sometimes “further towards the left” than
one would like. For example, in the following production:
declaration: modifier? variable { $startpos }
the keyword $startpos represents the start position of the optional
modifier modifier?. If this modifier turns out to be absent, then its
start position is (by definition) the end position of the most recently parsed
symbol. This may not be what is desired: perhaps the user would prefer in this
case to use the start position of the symbol variable. This is achieved by
using $symbolstartpos instead of $startpos. By definition,
$symbolstartpos is the start position of the leftmost symbol whose
start and end positions differ. In this example, the computation of
$symbolstartpos skips the absent modifier, whose start and end
positions coincide, and returns the start position of the symbol variable
(assuming this symbol has distinct start and end positions).
There is no keyword $symbolendpos. Indeed, the problem
with $startpos is due to the asymmetry in the definition
of $startpos and $endpos in the case of an empty right-hand
side, and does not affect $endpos.
The positions computed by Menhir are exactly the same as those computed by
ocamlyacc1. More precisely, Figure 15 sums up how
to translate a call to the Parsing module, as used in an ocamlyacc grammar, to a Menhir keyword.
We note that Menhir’s $startpos does not appear in the right-hand
column in Figure 15. In other words, Menhir’s $startpos
does not correspond exactly to any of the ocamlyacc function calls.
An exact ocamlyacc equivalent of $startpos is rhs_start_pos 1
if the current production has a nonempty right-hand side and
symbol_start_pos() if it has an empty right-hand side.
Finally, we remark that Menhir’s %inline keyword (§5.3) does not affect the computation of positions. The same positions are computed, regardless of where %inline keywords are placed.
When --interpret is set, Menhir no longer behaves as a compiler. Instead, it acts as an interpreter. That is, it repeatedly:
This process stops when the end of the input channel is reached.
The syntax of sentences is as follows:
| sentence | ::= | [ lid : ] uid … uid \n |
Less formally, a sentence is a sequence of zero or more terminal symbols (uid’s), separated with whitespace, terminated with a newline character, and optionally preceded with a non-terminal start symbol (lid). This non-terminal symbol can be omitted if, and only if, the grammar only has one start symbol.
For instance, here are four valid sentences for the grammar of arithmetic expressions found in the directory demos/calc:
main: INT PLUS INT EOL INT PLUS INT INT PLUS PLUS INT EOL INT PLUS PLUS
In the first sentence, the start symbol main was explicitly specified. In the other sentences, it was omitted, which is permitted, because this grammar has no start symbol other than main. The first sentence is a stream of four terminal symbols, namely INT, PLUS, INT, and EOL. These terminal symbols must be provided under their symbolic names. Writing, say, “12+32\n” instead of INT PLUS INT EOL is not permitted. Menhir would not be able to make sense of such a concrete notation, since it does not have a lexer for it.
As soon as Menhir is able to read a complete sentence off the standard input channel (that is, as soon as it finds the newline character that ends the sentence), it parses the sentence according to whichever grammar was specified on the command line, and displays an outcome.
An outcome is one of the following:
When --interpret-show-cst is set, each ACCEPT outcome is followed with a concrete syntax tree. A concrete syntax tree is either a leaf or a node. A leaf is either a terminal symbol or error. A node is annotated with a non-terminal symbol, and carries a sequence of immediate descendants that correspond to a valid expansion of this non-terminal symbol. Menhir’s notation for concrete syntax trees is as follows:
| cst | ::= | uid |
| error | ||
| [ lid : cst … cst ] |
For instance, if one wished to parse the example sentences of §8.1 using the grammar of arithmetic expressions in demos/calc, one could invoke Menhir as follows:
$ menhir --interpret --interpret-show-cst demos/calc/parser.mly main: INT PLUS INT EOL ACCEPT [main: [expr: [expr: INT] PLUS [expr: INT]] EOL] INT PLUS INT OVERSHOOT INT PLUS PLUS INT EOL REJECT INT PLUS PLUS REJECT
(Here, Menhir’s input—the sentences provided by the user on the standard input channel— is shown intermixed with Menhir’s output—the outcomes printed by Menhir on the standard output channel.) The first sentence is valid, and accepted; a concrete syntax tree is displayed. The second sentence is incomplete, because the grammar specifies that a valid expansion of main ends with the terminal symbol EOL; hence, the outcome is OVERSHOOT. The third sentence is invalid, because of the repeated occurrence of the terminal symbol PLUS; the outcome is REJECT. The fourth sentence, a prefix of the third one, is rejected for the same reason.
Using Menhir as an interpreter offers an easy way of debugging your grammar. For instance, if one wished to check that addition is considered left-associative, as requested by the %left directive found in the file demos/calc/parser.mly, one could submit the following sentence:
$ ./menhir --interpret --interpret-show-cst ../demos/calc/parser.mly INT PLUS INT PLUS INT EOL ACCEPT [main: [expr: [expr: [expr: INT] PLUS [expr: INT]] PLUS [expr: INT]] EOL ]
The concrete syntax tree displayed by Menhir is skewed towards the left, as desired.
The switches --interpret and --trace can be used in conjunction. When --trace is set, the interpreter logs its actions to the standard error channel.
When Menhir processes a grammar specification, say parser.mly, it
produces one OCaml module, Parser, whose code resides in the file
parser.ml and whose signature resides in the file
parser.mli. We now review this signature. For simplicity,
we assume that the grammar specification has just one start symbol
main, whose OCaml type is thing.
The monolithic API defines the type token, the exception Error,
and the parsing function main, named after the start symbol of the
grammar.
The type token is an algebraic data type. A value of type token
represents a terminal symbol and its semantic value. For instance, if the
grammar contains the declarations %token A and %token<int> B,
then the generated file parser.mli contains the following definition:
type token = | A | B of int
If --only-tokens is specified on the command line, the type token is
generated, and the rest is omitted. On the contrary, if --external-tokens is
used, the type token is omitted, but the rest (described below) is
generated.
The exception Error carries no argument. It is raised by the parsing
function main (described below) when a syntax error is detected.
exception Error
Next comes one parsing function for each start symbol of the grammar. Here, we
have assumed that there is one start symbol, named main, so the
generated file parser.mli contains the following declaration:
val main: (Lexing.lexbuf -> token) -> Lexing.lexbuf -> thing
This function expects two arguments, namely: a lexer, which typically is produced by
ocamllex and has type Lexing.lexbuf -> token; and a lexing buffer,
which has type Lexing.lexbuf. This API is compatible with
ocamlyacc. (For information on using Menhir without ocamllex, please
consult §16.)
This API is “monolithic” in the sense that there is just one function, which
does everything: it pulls tokens from the lexer, parses, and eventually
returns a semantic value (or fails by throwing the exception Error).
If --table is set, Menhir offers an incremental API in addition to the monolithic API. In this API, control is inverted. The parser does not have access to the lexer. Instead, when the parser needs the next token, it stops and returns its current state to the user. The user is then responsible for obtaining this token (typically by invoking the lexer) and resuming the parser from that state. The directory demos/calc-incremental contains a demo that illustrates the use of the incremental API.
This API is “incremental” in the sense that the user has access to a sequence of the intermediate states of the parser. Assuming that semantic values are immutable, a parser state is a persistent data structure: it can be stored and used multiple times, if desired. This enables applications such as “live parsing”, where a buffer is continuously parsed while it is being edited. The parser can be re-started in the middle of the buffer whenever the user edits a character. Because two successive parser states share most of their data in memory, a list of n successive parser states occupies only O(n) space in memory.
In this API, the parser is started by invoking
Incremental.main. (Recall that we assume that main is
the name of the start symbol.) The generated file parser.mli contains
the following declaration:
module Incremental : sig
val main: position -> thing MenhirInterpreter.checkpoint
end
The argument is the initial position. If the lexer is based on an OCaml lexing buffer, this argument should be lexbuf.lex_curr_p.
In §9.2 and §9.3,
the type position is a synonym for Lexing.position.
We emphasize that the function Incremental.main does not parse
anything. It constructs a checkpoint which serves as a starting
point. The functions offer and resume, described below, are used
to drive the parser.
The sub-module MenhirInterpreter is also part of the incremental API. Its declaration, which appears in the generated file parser.mli, is as follows:
module MenhirInterpreter : MenhirLib.IncrementalEngine.INCREMENTAL_ENGINE
with type token = token
The signature INCREMENTAL_ENGINE, defined in the module
MenhirLib.IncrementalEngine, contains many types and functions,
which are described in the rest of this section
(§9.2.2) and in the following sections
(§9.2.3, §9.2.4).
Please keep in mind that, from the outside, these types and functions should be referred
to with an appropriate prefix. For instance, the type checkpoint should be referred
to as MenhirInterpreter.checkpoint, or
Parser.MenhirInterpreter.checkpoint, depending on which modules the user
chooses to open.
type 'a env
The abstract type 'a env represents the current state of the
parser. (That is, it contains the current state and stack of the LR
automaton.) Assuming that semantic values are immutable, it is a persistent
data structure: it can be stored and used multiple times, if desired.
The parameter 'a is the type of the semantic value that will
eventually be produced if the parser succeeds.
type production
The abstract type production represents a production of the grammar.
The “start productions” (which do not exist in an .mly file, but are
constructed by Menhir internally) are not part of this type.
type 'a checkpoint = private
| InputNeeded of 'a env
| Shifting of 'a env * 'a env * bool
| AboutToReduce of 'a env * production
| HandlingError of 'a env
| Accepted of 'a
| Rejected
The type 'a checkpoint represents an intermediate or
final state of the parser. An intermediate checkpoint is a suspension: it records
the parser’s current state, and allows parsing to be resumed. The parameter
'a is the type of the semantic value that will eventually be produced
if the parser succeeds.
Accepted and Rejected are final checkpoints. Accepted carries
a semantic value.
InputNeeded is an intermediate checkpoint. It means that the parser wishes
to read one token before continuing.
Shifting is an intermediate checkpoint. It means that the parser is taking
a shift transition. It exposes the state of the parser before and after the
transition. The Boolean parameter tells whether the parser intends to request
a new token after this transition. (It always does, except when it is about to
accept.)
AboutToReduce is an intermediate checkpoint: it means that the parser is
about to perform a reduction step. HandlingError is also an
intermediate checkpoint: it means that the parser has detected an error and is
about to handle it. (Error handling is typically performed in several steps,
so the next checkpoint is likely to be HandlingError again.) In these two
cases, the parser does not need more input. The parser suspends itself at this
point only in order to give the user an opportunity to observe the parser’s
transitions and possibly handle errors in a different manner, if desired.
val offer:
'a checkpoint ->
token * position * position ->
'a checkpoint
The function offer allows the user to resume the parser after the
parser has suspended itself with a checkpoint of the form InputNeeded env.
This function expects the previous checkpoint checkpoint as well as a new token
(together with the start and end positions of this token). It produces a new
checkpoint, which again can be an intermediate checkpoint or a final checkpoint. It does
not raise any exception. (The exception Error is used only in the
monolithic API.)
val resume:
?strategy:[ `Legacy | `Simplified ] ->
'a checkpoint ->
'a checkpoint
The function resume allows the user to resume the parser after the
parser has suspended itself with a checkpoint of the form
Shifting _ or AboutToReduce _ or HandlingError _.
This function expects just the previous checkpoint checkpoint. It produces a new
checkpoint. It does not raise any exception.
The optional argument strategy influences the manner in which
resume deals with checkpoints of the form HandlingError _. Its
default value is `Legacy. For more details, see §10.
The incremental API subsumes the monolithic API. Indeed, main can be
(and is in fact) implemented by first using
Incremental.main, then calling offer and
resume in a loop, until a final checkpoint is obtained.
type supplier =
unit -> token * position * position
A token supplier is a function of no arguments which delivers a new token
(together with its start and end positions) every time it is called. The
function loop and its variants, described below, expect a supplier
as an argument.
val lexer_lexbuf_to_supplier:
(Lexing.lexbuf -> token) -> Lexing.lexbuf -> supplier
The function lexer_lexbuf_to_supplier, applied to a lexer and to a
lexing buffer, produces a fresh supplier.
The functions offer and resume, documented above, are sufficient
to write a parser loop. One can imagine many variations of such a loop, which
is why we expose offer and resume in the first place.
Nevertheless, some variations are so common that it is worth providing them,
ready for use. The following functions are implemented on top of offer
and resume.
val loop:
?strategy:[ `Legacy | `Simplified ] ->
supplier -> 'a checkpoint -> 'a
loop supplier checkpoint begins parsing from checkpoint, reading
tokens from supplier. It continues parsing until it reaches a
checkpoint of the form Accepted v or Rejected. In the former
case, it returns v. In the latter case, it raises the
exception Error. (By the way, this is how we implement the monolithic
API on top of the incremental API.)
The optional argument strategy influences the manner in which
loop deals with checkpoints of the form HandlingError _. Its
default value is `Legacy. For more details, see §10.
val loop_handle:
('a -> 'answer) ->
('a checkpoint -> 'answer) ->
supplier -> 'a checkpoint -> 'answer
loop_handle succeed fail supplier checkpoint begins parsing from
checkpoint, reading tokens from supplier. It continues until
it reaches a checkpoint of the form Accepted v or HandlingError _
(or Rejected, but that should not happen, as HandlingError _
will be observed first). In the former case, it calls succeed v. In
the latter case, it calls fail with this checkpoint. It cannot
raise Error.
This means that Menhir’s traditional error-handling procedure (which pops the
stack until a state that can act on the error token is found) does not get a
chance to run. Instead, the user can implement her own error-handling code, in
the fail continuation.
val loop_handle_undo:
('a -> 'answer) ->
('a checkpoint -> 'a checkpoint -> 'answer) ->
supplier -> 'a checkpoint -> 'answer
loop_handle_undo is analogous to loop_handle, but passes a pair
of checkpoints (instead of a single checkpoint) to the failure continuation.
The first (and oldest) checkpoint that is passed to the failure continuation
is the last InputNeeded checkpoint that was encountered before the
error was detected. The second (and newest) checkpoint is where the error was
detected. (This is the same checkpoint that loop_handle would pass to
its failure continuation.) Going back to the first checkpoint can be thought
of as undoing any reductions that were performed after seeing the problematic
token. (These reductions must be default reductions or spurious reductions.)
This can be useful to someone who wishes to implement an error explanation or
error recovery mechanism.
loop_handle_undo must be applied to an InputNeeded checkpoint.
The initial checkpoint produced by Incremental.main is of this form.
val shifts: 'a checkpoint -> 'a env option
shifts checkpoint assumes that checkpoint has been obtained by
submitting a token to the parser. It runs the parser from checkpoint,
through an arbitrary number of reductions, until the parser either accepts
this token (i.e., shifts) or rejects it (i.e., signals an error). If the
parser decides to shift, then Some env is returned, where env is
the parser’s state just before shifting. Otherwise, None is returned.
This can be used to test whether the parser is willing to accept a certain
token. This function should be used with caution, though, as it causes
semantic actions to be executed. It is desirable that all semantic actions be
side-effect-free, or that their side-effects be harmless.
val acceptable: 'a checkpoint -> token -> position -> bool
acceptable checkpoint token pos requires checkpoint to be an
InputNeeded checkpoint. It returns true iff the parser is
willing to shift this token.
This can be used to test, after an error has been detected, which tokens would
have been accepted at this point. To do this, one would typically use
loop_handle_undo to get access to the last InputNeeded
checkpoint that was encountered before the error was detected, and apply
acceptable to that checkpoint.
acceptable is implemented using shifts, so, like shifts,
it causes certain semantic actions to be executed. It is desirable that all
semantic actions be side-effect-free, or that their side-effects be harmless.
Although the type env is opaque, a parser state can be inspected via a
few accessor functions, which are described in this section. The following
types and functions are contained in the MenhirInterpreter sub-module.
type 'a lr1state
The abstract type 'a lr1state describes a (non-initial) state of the
LR(1) automaton.
If s is such a state, then s should have at least one incoming
transition, and all of its incoming transitions carry the same (terminal or
non-terminal) symbol, say A. We say that A is the incoming symbol
of the state s.
The index 'a is the type of the semantic values associated with A.
The role played by 'a is clarified in the definition of the
type element, which appears further on.
val number: _ lr1state -> int
The states of the LR(1) automaton are numbered (from 0 and up).
The function number maps a state to its number.
val production_index: production -> int val find_production: int -> production
Productions are numbered. (The set of indices of all productions forms an
interval, which does not necessarily begin at 0.)
The function production_index converts a production to an integer
number, whereas the function find_production carries out the reverse
conversion. It is an error to apply find_production to an invalid
index.
type element =
| Element: 'a lr1state * 'a * position * position -> element
The type element describes one entry in the stack of the LR(1)
automaton. In a stack element of the form Element (s, v, startp, endp),
s is a (non-initial) state and v is a semantic value. The
value v is associated with the incoming symbol A of the
state s. In other words, the value v was pushed onto the stack
just before the state s was entered. Thus, for some type 'a, the
state s has type 'a lr1state and the value v has
type 'a. The positions startp and endp delimit the
fragment of the input text that was reduced to the symbol A.
In order to do anything useful with the value v, one must gain
information about the type 'a, by inspection of the state s. So
far, the type 'a lr1state is abstract, so there is no way of
inspecting s. The inspection API (§9.3) offers further
tools for this purpose.
val top: 'a env -> element option
top env returns the parser’s top stack element. The state contained in
this stack element is the current state of the automaton. If the stack is
empty, None is returned. In that case, the current state of the
automaton must be an initial state.
val pop_many: int -> 'a env -> 'a env option
pop_many i env pops i elements off the automaton’s stack. This
is done via i successive invocations of pop. Thus,
pop_many 1 is pop. The index i must be nonnegative. The
time complexity is O(i).
val get: int -> 'a env -> element option
get i env returns the parser’s i-th stack element. The index
i is 0-based: thus, get 0 is top. If i is greater
than or equal to the number of elements in the stack, None is returned.
get is implemented using pop_many and top: its time
complexity is O(i).
val current_state_number: 'a env -> int
current_state_number env is the integer number of the automaton’s
current state. Although this number might conceivably be obtained via the
functions top and number, using current_state_number is
preferable, because this method works even when the automaton’s stack is empty
(in which case the current state is an initial state, and top returns
None). This number can be passed as an argument to a message
function generated by menhir --compile-errors.
val equal: 'a env -> 'a env -> bool
equal env1 env2 tells whether the parser configurations env1 and
env2 are equal in the sense that the automaton’s current state is the
same in env1 and env2 and the stack is physically the
same in env1 and env2. If equal env1 env2 is true,
then the sequence of the stack elements, as observed via pop and
top, must be the same in env1 and env2. Also, if
equal env1 env2 holds, then the checkpoints input_needed env1
and input_needed env2 must be equivalent. (The function
input_needed is documented in §9.2.4.)
The function equal has time complexity O(1).
val positions: 'a env -> position * position
The function positions returns the start and end positions of the
current lookahead token. If invoked in an initial state, this function returns
a pair of twice the initial position that was passed as an argument
to main.
val env_has_default_reduction: 'a env -> bool val state_has_default_reduction: _ lr1state -> bool
When applied to an environment env taken from a checkpoint of the form
AboutToReduce (env, prod), the function
env_has_default_reduction tells whether the reduction that is about to
take place is a default reduction.
state_has_default_reduction s tells whether the state s has a default
reduction. This includes the case where s is an accepting state.
The functions presented in the previous section
(§9.2.3) allow inspecting parser states of type
'a checkpoint and 'a env. However, so far, there are no
functions for manufacturing new parser states, except offer and
resume, which create new checkpoints by feeding tokens, one by one, to
the parser.
In this section, a small number of functions are provided for manufacturing
new parser states of type 'a env and 'a checkpoint. These
functions allow going far back into the past and jumping ahead into the
future, so to speak. In other words, they allow driving the parser in other
ways than by feeding tokens into it. The functions pop,
force_reduction and feed (part of the inspection API; see
§9.3) construct values of type 'a env. The function
input_needed constructs values of type 'a checkpoint and thereby
allows resuming parsing in normal mode (via offer). Together, these
functions can be used to implement error handling and error recovery
strategies.
val pop: 'a env -> 'a env option
pop env returns a new environment, where the parser’s top stack cell
has been popped off. (If the stack is empty, None is returned.) This
amounts to pretending that the (terminal or nonterminal) symbol that
corresponds to this stack cell has not been read.
val force_reduction: production -> 'a env -> 'a env
force_reduction prod env can be called only if in the state env
the parser is capable of reducing the production prod. If this
condition is satisfied, then this production is reduced, which means that its
semantic action is executed (this can have side effects!) and the automaton
makes a goto (nonterminal) transition. If this condition is not satisfied, an
Invalid_argument exception is raised.
val input_needed: 'a env -> 'a checkpoint
input_needed env returns InputNeeded env. Thus, out of a parser
state that might have been obtained via a series of calls to the functions
pop, force_reduction, feed, and so on, it produces a
checkpoint, which can be used to resume normal parsing, by supplying this
checkpoint as an argument to offer.
This function should be used with some care. It could “mess up the
lookahead” in the sense that it allows parsing to resume in an arbitrary
state s with an arbitrary lookahead symbol t, even though
Menhir’s reachability analysis (which is carried out via the --list-errors switch) might well think that it is impossible to reach this particular
configuration. If one is using Menhir’s new error reporting facility
(§11), this could cause the parser to reach an error state
for which no error message has been prepared.
If --inspection is set, Menhir offers an inspection API in addition to the monolithic and incremental APIs. (The reason why this is not done by default is that this requires more tables to be generated, thus making the generated parser larger.) Like the incremental API, the inspection API is found in the sub-module MenhirInterpreter. It offers the following types and functions.
The type 'a terminal is a generalized algebraic data type (GADT). A
value of type 'a terminal represents a terminal symbol (without a
semantic value). The index 'a is the type of the semantic values
associated with this symbol. For instance, if the grammar contains the
declarations %token A and %token<int> B, then the generated
module MenhirInterpreter contains the following definition:
type _ terminal = | T_A : unit terminal | T_B : int terminal
The data constructors are named after the terminal symbols, prefixed with “T_”.
The type 'a nonterminal is also a GADT. A value of type
'a nonterminal represents a nonterminal symbol (without a semantic value). The
index 'a is the type of the semantic values associated with this
symbol. For instance, if main is the only nonterminal symbol,
then the generated
module MenhirInterpreter contains the following definition:
type _ nonterminal = | N_main : thing nonterminal
The data constructors are named after the nonterminal symbols, prefixed with “N_”.
The type 'a symbol
is the disjoint union of the types 'a terminal and 'a nonterminal.
In other words, a value of type 'a symbol represents a terminal or nonterminal symbol (without
a semantic value).
This type is (always) defined as follows:
type 'a symbol =
| T : 'a terminal -> 'a symbol
| N : 'a nonterminal -> 'a symbol
The type xsymbol is an existentially quantified version of the
type 'a symbol. It is useful in situations where the index 'a is
not statically known. It is (always) defined as follows:
type xsymbol =
| X : 'a symbol -> xsymbol
The type item describes an LR(0) item, that is, a pair of a production
prod and an index i into the right-hand side of this production.
If the length of the right-hand side is n, then i is
comprised between 0 and n, inclusive.
type item =
production * int
The following functions implement total orderings on the types
_ terminal, _ nonterminal, xsymbol,
production, and item.
val compare_terminals: _ terminal -> _ terminal -> int val compare_nonterminals: _ nonterminal -> _ nonterminal -> int val compare_symbols: xsymbol -> xsymbol -> int val compare_productions: production -> production -> int val compare_items: item -> item -> int
The function incoming_symbol maps a (non-initial) LR(1)
state s to its incoming symbol, that is, the symbol that the parser
must recognize before it enters the state s.
val incoming_symbol: 'a lr1state -> 'a symbol
This function can be used to gain access to the semantic value v
in a stack element Element (s, v, _, _). Indeed, by case analysis on the
symbol incoming_symbol s, one gains information about the type 'a,
hence one obtains the ability to do something useful with the value v.
The function items maps a (non-initial) LR(1) state s to its
LR(0) core, that is, to the underlying set of LR(0) items. This set
is represented as a list, whose elements appear in an arbitrary order. This
set is not closed under є-transitions.
val items: _ lr1state -> item list
The functions lhs and rhs map a production prod to
its left-hand side and right-hand side, respectively. The left-hand side
is always a nonterminal symbol, hence always of the form N _. The
right-hand side is a (possibly empty) sequence of (terminal or nonterminal)
symbols.
val lhs: production -> xsymbol val rhs: production -> xsymbol list
The function nullable, applied to a non-terminal symbol,
tells whether this symbol is nullable. A nonterminal symbol is nullable if and
only if it produces the empty word є.
val nullable: _ nonterminal -> bool
The function call first nt t tells whether the FIRST set of the
nonterminal symbol nt contains the terminal symbol t. That is,
it returns true if and only if nt produces a word that begins
with t. The function xfirst is identical to first, except
it expects a first argument of type xsymbol instead of _ terminal.
val first: _ nonterminal -> _ terminal -> bool val xfirst: xsymbol -> _ terminal -> bool
The function foreach_terminal enumerates the terminal symbols, including the special symbol error.
The function foreach_terminal_but_error enumerates the terminal symbols, excluding error.
val foreach_terminal: (xsymbol -> 'a -> 'a) -> 'a -> 'a val foreach_terminal_but_error: (xsymbol -> 'a -> 'a) -> 'a -> 'a
feed symbol startp semv endp env causes the parser to consume the
(terminal or nonterminal) symbol symbol, accompanied with the semantic
value semv and with the start and end positions startp and
endp. Thus, the automaton makes a transition, and reaches a new state.
The stack grows by one cell. This operation is permitted only if the current
state (as determined by env) has an outgoing transition labeled with
symbol. Otherwise, an Invalid_argument exception is raised.
val feed: 'a symbol -> position -> 'a -> position -> 'b env -> 'b env
The purpose of parsing is to transform a sequence of characters, or a sequence of tokens, into a semantic value, which typically is some kind of syntax tree. The purpose of unparsing is to perform the reverse transformation, that is, to transform a syntax tree back into a sequence of tokens or characters.
Although unparsing may not seem conceptually very challenging, writing an unparser by hand can require a significant amount of work. Furthermore, ensuring that an unparser is correct can be difficult. An unparser is correct if its output can be parsed and if this gives rise to the same syntax tree that one started with. In other words, it is correct if the composition unparse; parse is the identity. Intuitively, this means that the unparser must produce syntactically correct output and must insert enough parentheses (or other disambiguation symbols) to ensure that its output is correctly interpreted. If the grammar involves priority or precedence declarations (§4.1.4, §4.2.1), enforcing this property can be tricky.
When the switch --unparsing is supplied on the command line, Menhir generates code that helps implement a correct unparser. In this reference manual, we give a brief overview of the generated code; for more details, the reader is referred to the paper “Correct, Fast LR(1) Unparsing” [22]. Furthermore, the directory demos/calc-unparsing contains a demo that illustrates the use of the unparsing API. In this directory, the command make api shows the file parser.mli generated by Menhir.
The unparsing API involves two distinct data structures, namely disjunctive concrete syntax trees and concrete syntax trees.
The unparsing API expects the unparsing process to be performed in three steps, as follows:
The facilities provided by the unparsing API are:
The settlement algorithm performs step 2 automatically. It is up to you, the user, to implement steps 1 and 2. In step 2, you use the DCST construction API. In step 3, you use the CST deconstruction API.
The DST construction API is found in the sub-module DCST. It offers a set of constructor functions that you can use to construct DCSTs. OCaml’s type discipline ensures that only well-formed DCSTs can be constructed; this rules out a class of mistakes that would lead to syntactically incorrect output.
type expr
expr:
LPAREN; e = expr; RPAREN { e } [@name paren]
then the sub-module DCST includes a constructor function
val paren: expr -> expr
val expr_choice: expr -> expr -> expr
For each start nonterminal symbol, say main, there is a function, named Settle.main, which transforms a DCST to a CST.
val main: DCST.main -> CST.main option
This transformation eliminates all disjunction nodes. In other words, whenever there is a choice between several ways of displaying a subtree (for example, without or with surrounding parentheses), this choice is resolved. The settlement algorithm is left-biased: if the left-hand alternative leads to a viable tree (that is, a tree that can be printed and parsed again, without confusion) then this alternative is chosen; otherwise, the right-hand alternative is chosen.
If the algorithm is unable to find a viable tree, then it fails: it returns None. If you encounter this situation, first make sure that in the previous step (step 1) you have inserted enough parentheses, or constructed enough disjunction nodes that offer a possibility of inserting parentheses. If you think that you have done so, and if the algorithm still fails, please contact Menhir’s developers. As explained in the paper [22], the settlement algorithm is fast but incomplete. When faced with a disjunction node, it commits early to the left-hand alternative. If this alternative later turns out to fail, then the algorithm does not backtrack; the right-hand alternative is never tried.
The CST deconstruction API is found in the sub-module CST. It offers a visitor class, named reduce, which allows traversing a CST and transforming it into a printable form. This printable form could be text, or could be a document in a a structured document description language; it is up to the user to choose it.
For each nonterminal symbol, say expr, there is an abstract type of CSTs, also named expr.
type expr
Then, there is a single visitor class:
class virtual ['r] reduce : object
method virtual zero : 'r
method virtual cat : 'r -> 'r -> 'r
method virtual text : string -> 'r
(* one method per terminal symbol *)
(* one method per nonterminal symbol *)
(* one method per production *)
end
This class is parameterized by a type ’r, which is the result type of every method: it is the type of the printable form to which every tree must be reduced.
The user is expected to provide implementations for the three virtual methods zero, cat, and text. In short, zero is the empty printable thing; cat concatenates two printable things; and text converts a string to a printable thing.
Furthermore, the following methods exist:
%token<int> INT
then the following method exists:
method virtual visit_INT : int -> 'rThis method is normally virtual. However, if the terminal symbol carries no semantic value and if a token alias (§4.1.3) has been provided by the user for this symbol then a default implementation of this method is generated by Menhir ; the method is then non-virtual. For example, if the token LPAREN has been declared by
%token LPAREN "("
then the following non-virtual method exists:
method visit_LPAREN : 'r
method visit_expr : expr -> 'r
expr:
LPAREN; e = expr; RPAREN { e } [@name paren]
then the following method exists:
method case_paren : expr -> 'r
Menhir’s traditional error-handling mechanism is considered deprecated: although it is still supported for the time being, it is likely to be removed in the future. We recommend setting up an error-handling mechanism using the new tools offered by Menhir (§11).
Menhir’s error traditional handling mechanism is inspired by that of yacc and ocamlyacc, but is not identical. A special error token is made available for use within productions. The LR automaton is constructed exactly as if error was a regular terminal symbol. However, error is never produced by the lexical analyzer. Instead, when an error is detected, the current lookahead token is discarded and replaced with the error token, which becomes the current lookahead token. At this point, the parser enters error handling mode. In error-handling mode, the parser behaves as follows:
In the monolithic API, the parser rejects the input by raising the exception Error. This exception carries no information. The position of the error can be obtained by reading the lexical analyzer’s environment record. In the incremental API, the parser rejects the input by returning the checkpoint Rejected.
Which strategy should one choose? First, let us note that the difference between the strategies legacy and simplified matters only if the grammar uses the error token. The following rule of thumb can be used to select between them:
ocamlyacc offers an error recovery mode, which is entered immediately after an error token was successfully shifted. In this mode, tokens are repeatedly taken off the input stream and discarded until an acceptable token is found. This feature is no longer offered by Menhir.
Menhir’s incremental API (§9.2) allows taking control when
an error is detected. Indeed, as soon as an invalid token is detected, the
parser produces a checkpoint of the form HandlingError _. At this
point, if one decides to let the parser proceed, by just
calling resume, then Menhir enters its traditional error-handling mode
(§10). Instead, however, one can decide to take control and
perform error handling or error recovery in any way one pleases. One can, for
instance, build and display a diagnostic message, based on the automaton’s
current stack and/or state. Or, one could modify the input stream, by
inserting or deleting tokens, so as to suppress the error, and resume normal
parsing. In principle, the possibilities are endless.
An apparently simple-minded approach to error reporting, proposed by Jeffery [11] and further explored by Pottier [21], consists in selecting a diagnostic message (or a template for a diagnostic message) based purely on the current state of the automaton.
In this approach, one determines, ahead of time, which are the “error states” (that is, the states in which an error can be detected), and one prepares, for each error state, a diagnostic message. Because state numbers are fragile (they change when the grammar evolves), an error state is identified not by its number, but by an input sentence that leads to it: more precisely, by an input sentence which causes an error to be detected in this state. Thus, one maintains a set of pairs of an erroneous input sentence and a diagnostic message.
Menhir defines a file format, the .messages file format, for representing this information (§11.1), and offers a set of tools for creating, maintaining, and exploiting .messages files (§11.2). Once one understands these tools, there remains to write a collection of diagnostic messages, a more subtle task than one might think (§11.3), and to glue everything together (§11.4).
In this approach to error handling, as in any other approach, one must understand exactly when (that is, in which states) errors are detected. This in turn requires understanding how the automaton is constructed. Menhir’s construction technique is not Knuth’s canonical LR(1) technique [16], which is usually too expensive to be practical. Instead, Menhir merges states [20] and introduces so-called default reductions. These techniques defer error detection by allowing extra reductions to take place before an error is detected. The impact of these alterations must be taken into account when writing diagnostic messages (§11.3).
In this approach to error handling, the special error token is not used. It should not appear in the grammar.
A .messages file is a text file. It is composed of a list of entries. Each entry consists of one or more input sentences, followed with one or more blank lines, followed with a message. Two entries are separated by one or more blank lines. The syntax of an input sentence is described in §8.1. A message is an arbitrary piece of text, but cannot cannot a blank line.
Blank lines are significant: they are used as separators, both between entries, and (within an entry) between the sentences and the message. Thus, there cannot be a blank line between two sentences. (If there is one, Menhir becomes confused and may complain about some word not being “a known non-terminal symbol”). There also cannot be a blank line inside a message.
grammar: TYPE UID # This hand-written comment concerns just the sentence above. grammar: TYPE OCAMLTYPE UID PREC # This hand-written comment concerns just the sentence above. # This hand-written comment concerns both sentences above. Ill-formed declaration. Examples of well-formed declarations: %type <Syntax.expression> expression %type <int> date time
Figure 16: An entry in a .messages file
grammar: TYPE UID ## ## Ends in an error in state: 1. ## ## declaration -> TYPE . OCAMLTYPE separated_nonempty_list(option(COMMA), ## strict_actual) [ TYPE TOKEN START RIGHT PUBLIC PERCENTPERCENT PARAMETER ## ON_ERROR_REDUCE NONASSOC LEFT INLINE HEADER EOF COLON ] ## ## The known suffix of the stack is as follows: ## TYPE ## # This hand-written comment concerns just the sentence above. # grammar: TYPE OCAMLTYPE UID PREC ## ## Ends in an error in state: 5. ## ## strict_actual -> symbol . loption(delimited(LPAREN,separated_nonempty_list ## (COMMA,strict_actual),RPAREN)) [ UID TYPE TOKEN START STAR RIGHT QUESTION ## PUBLIC PLUS PERCENTPERCENT PARAMETER ON_ERROR_REDUCE NONASSOC LID LEFT ## INLINE HEADER EOF COMMA COLON ] ## ## The known suffix of the stack is as follows: ## symbol ## # This hand-written comment concerns just the sentence above. # This hand-written comment concerns both sentences above. Ill-formed declaration. Examples of well-formed declarations: %type <Syntax.expression> expression %type <int> date time
Figure 17: An entry in a .messages file, decorated with auto-generated comments
As an example, Figure 16 shows a valid entry, taken from Menhir’s own .messages file. This entry contains two input sentences, which lead to errors in two distinct states. A single message is associated with these two error states.
Comment lines, which begin with a # character, are ignored everywhere.
However, users who wish to take advantage of Menhir’s facility for merging
two .messages files (§11.2) should follow certain
conventions regarding the placement of comments:
Several commands, described next (§11.2),
produce .messages files where each input sentence is followed with an
auto-generated comment, marked with ##. This special comment indicates
in which state the error is detected, and is supposed to help the reader
understand what it means to be in this state: What has been read so far? What
is expected next?
As an example, the previous entry, decorated with auto-generated comments, is shown in Figure 17. (We have manually wrapped the lines that did not fit in this document.)
An auto-generated comment begins with the number of the error state that is reached via this input sentence.
Then, the auto-generated comment shows the LR(1) items that compose this state, in the same format as in an .automaton file. these items offer a description of the past (that is, what has been read so far) and the future (that is, which terminal symbols are allowed next).
Finally, the auto-generated comment shows what is known about the stack when the automaton is in this state. (This can be deduced from the LR(1) items, but is more readable if shown separately.)
In a canonical LR(1) automaton, the LR(1) items offer an exact description of the past and future. However, in a noncanonical automaton, which is by default what Menhir produces, the situation is more subtle. The lookahead sets can be over-approximated, so the automaton can perform one or more “spurious reductions” before an error is detected. As a result, the LR(1) items in the error state offer a description of the future that may be both incorrect (that is, a terminal symbol that appears in a lookahead set is not necessarily a valid continuation) and incomplete (that is, a terminal symbol that does not appear in any lookahead set may nevertheless be a valid continuation). More details appear further on (§11.3).
In order to attract the user’s attention to this issue, if an input sentence causes one or more spurious reductions, then the auto-generated comment contains a warning about this fact. This mechanism is not completely foolproof, though, as it may be the case that one particular sentence does not cause any spurious reductions (hence, no warning appears), yet leads to an error state that can be reached via other sentences that do involve spurious reductions.
Ideally, the set of input sentences in a .messages file should be correct (that is, every sentence causes an error on its last token), irredundant (that is, no two sentences lead to the same error state), and complete (that is, every error state is reached by some sentence).
The correctness and irredundancy of a .messages file are checked by supplying
--compile-errors filename on the command line, where filename is the
name of the .messages file. (These arguments must be supplied in addition to
the other usual arguments, such as the name of the .mly file.) This command
fails if a sentence does not cause an error at all, or causes an error too
early. It also fails if two sentences lead to the same error state.
If the file is correct and irredundant, then (as its name suggests) this
command compiles the .messages file down to an OCaml function, whose code
is printed on the standard output channel. This function, named message,
has type int -> string, and maps a state number to a message. It
raises the exception Not_found if its argument is not the number of
a state for which a message has been defined. If the set of input sentences
is complete, then it cannot raise Not_found.
The completeness of a .messages file is checked via the commands --list-errors and --compare-errors. The former produces, from scratch, a complete set of input sentences, that is, a set of input sentences that reaches all error states. The latter compares two sets of sentences (more precisely, the two underlying sets of error states) for inclusion.
The command --list-errors first computes all possible ways of causing an error. From this information, it deduces a list of all error states, that is, all states where an error can be detected. For each of these states, it computes a (minimal) input sentence that causes an error in this state. Finally, it prints these sentences, in the .messages file format, on the standard output channel. Each sentence is followed with an auto-generated comment and with a dummy diagnostic message. The user should be warned that this algorithm may require large amounts of time (typically in the tens of seconds, possibly more) and memory (typically in the gigabytes, possibly more). It requires a 64-bit machine. (On a 32-bit machine, it works, but quickly hits a built-in size limit.) At the verbosity level --log-automaton 2, it displays some progress information and internal statistics on the standard error channel.
The command --compare-errors filename1 --compare-errors filename2 compares the .messages files filename1 and filename2. Each file is read and internally translated to a mapping of states to messages. Menhir then checks that the left-hand mapping is a subset of the right-hand mapping. That is, if a state s is reached by some sentence in filename1, then it should also be reached by some sentence in filename2. Furthermore, if the message associated with s in filename1 is not a dummy message, then the same message should be associated with s in filename2.
To check that the sentences in filename2 cover all error states, it suffices to (1) use --list-errors to produce a complete set of sentences, which one stores in filename1, then (2) use --compare-errors to compare filename1 and filename2.
In the case of a grammar that evolves fairly often, it can take significant
human time and effort to update the .messages file and ensure correctness,
irredundancy, and completeness. A tempting way of reducing this effort is to abandon
completeness. This implies that the auto-generated message function can
raise Not_found and that a generic “syntax error” message must be
produced in that case. We prefer to discourage this approach, as it implies
that the end user is exposed to a mixture of specific and generic syntax error
messages, and there is no guarantee that the specific (hand-written) messages
will appear in all situations where they are expected to appear.
Instead, we recommend waiting for the grammar to become stable and enforcing
completeness.
The command --merge-errors filename1 --merge-errors filename2 attempts to merge the .messages files filename1 and filename2, and prints the result on the standard output channel. This command can be useful if two users have worked independently and each of them has produced a .messages file that covers a subset of all error states. The merging algorithm works roughly as follows:
<YOUR SYNTAX ERROR MESSAGE HERE> is ignored.
The algorithm is asymmetric: the content of filename1 is inserted into or appended to filename2. For this reason, if one of the files is a large “reference” file and the other file is a small “delta”, then it is recommended to provide the “delta” as filename1 and the “reference” as filename2.
The command --update-errors filename is used to update the auto-generated
comments in the .messages file filename. It is typically used after a
change in the grammar (or in the command line options that affect the
construction of the automaton). A new .messages file is produced on the
standard output channel. It is identical to filename, except the
auto-generated comments, identified by ##, have been removed and
re-generated.
The command --echo-errors filename is used to filter out all comments, blank lines, and messages from the .messages file filename. The input sentences, and nothing else, are echoed on the standard output channel. As an example application, one could then translate the sentences to concrete syntax and create a collection of source files that trigger every possible syntax error.
The command --interpret-error is analogous to --interpret. It causes Menhir to act as an interpreter. Menhir reads sentences off the standard input channel, parses them, and displays the outcome. This switch can be usefully combined with --trace. The main difference between --interpret and --interpret-error is that, when the latter command is used, Menhir expects the input sentence to cause an error on its last token, and displays information about the state in which the error is detected, in the form of a .messages file entry. This can be used to quickly find out exactly what error is caused by one particular input sentence.
One might think that writing a diagnostic message for each error state is a straightforward (if lengthy) task. In reality, it is not so simple.
The first thing to keep in mind is that a diagnostic message is associated with a state s, as opposed to a sentence. An entry in a .messages file contains a sentence w that leads to an error in state s. This sentence is just one way of causing an error in state s; there may exist many other sentences that also cause an error in this state. The diagnostic message should not be specific of the sentence w: it should make sense regardless of how the state s is reached.
As a rule of thumb, when writing a diagnostic message, one should (as much as possible) ignore the example sentence w altogether, and concentrate on the description of the state s, which appears as part of the auto-generated comment.
The LR(1) items that compose the state s offer a description of the past (that is, what has been read so far) and the future (that is, which terminal symbols are allowed next). A diagnostic message should be designed based on this description.
%token ID ARROW LPAREN RPAREN COLON SEMICOLON %start<unit> program %% typ0: ID | LPAREN typ1 RPAREN {} typ1: typ0 | typ0 ARROW typ1 {} declaration: ID COLON typ1 {} program: | LPAREN declaration RPAREN | declaration SEMICOLON {}
Figure 18: A grammar where one error state is difficult to explain
program: ID COLON ID LPAREN ## ## Ends in an error in state: 8. ## ## typ1 -> typ0 . [ SEMICOLON RPAREN ] ## typ1 -> typ0 . ARROW typ1 [ SEMICOLON RPAREN ] ## ## The known suffix of the stack is as follows: ## typ0 ##
Figure 19: A problematic error state in the grammar of Figure 18, due to over-approximation
As pointed out earlier (§11.1), in a noncanonical automaton, the lookahead sets in the LR(1) items can be both over- and under-approximated. One must be aware of this phenomenon, otherwise one runs the risk of writing a diagnostic message that proposes too many or too few continuations.
As an example, let us consider the grammar in Figure 18. According to this grammar, a “program” is either a declaration between parentheses or a declaration followed with a semicolon. A “declaration” is an identifier, followed with a colon, followed with a type. A “type” is an identifier, a type between parentheses, or a function type in the style of OCaml.
The (noncanonical) automaton produced by Menhir for this grammar has 17 states. Using --list-errors, we find that an error can be detected in 10 of these 17 states. By manual inspection of the auto-generated comments, we find that for 9 out of these 10 states, writing an accurate diagnostic message is easy. However, one problematic state remains, namely state 8, shown in Figure 19.
In this state, a (level-0) type has just been read. One valid continuation,
which corresponds to the second LR(1) item in Figure 19,
is to continue this type: the terminal symbol ARROW, followed with a
(level-1) type, is a valid continuation. Now, the question is, what other
valid continuations are there? By examining the first LR(1) item
in Figure 19, it may look as if both SEMICOLON
and RPAREN are valid continuations. However, this cannot be the case. A
moment’s thought reveals that either we have seen an opening
parenthesis LPAREN at the very beginning of the program, in which case
we definitely expect a closing parenthesis RPAREN; or we have
not seen one, in which case we definitely expect a semicolon SEMICOLON.
It is never the case that both SEMICOLON
and RPAREN are valid continuations!
In fact, the lookahead set in the first LR(1) item in Figure 19 is over-approximated. State 8 in the noncanonical automaton results from merging two states in the canonical automaton.
In such a situation, one cannot write an accurate diagnostic message.
Knowing that the automaton is in state 8 does not give us a
precise view of the valid continuations. Some valuable information (that is,
whether we have seen an opening parenthesis LPAREN at the very
beginning of the program) is buried in the automaton’s stack.
%token ID ARROW LPAREN RPAREN COLON SEMICOLON %start<unit> program %% typ0: ID | LPAREN typ1(RPAREN) RPAREN {} typ1(phantom): typ0 | typ0 ARROW typ1(phantom) {} declaration(phantom): ID COLON typ1(phantom) {} program: | LPAREN declaration(RPAREN) RPAREN | declaration(SEMICOLON) SEMICOLON {}
Figure 20: Splitting the problematic state of Figure 19 via selective duplication
%token ID ARROW LPAREN RPAREN COLON SEMICOLON %start<unit> program %on_error_reduce typ1 %% typ0: ID | LPAREN typ1 RPAREN {} typ1: typ0 | typ0 ARROW typ1 {} declaration: ID COLON typ1 {} program: | LPAREN declaration RPAREN | declaration SEMICOLON {}
Figure 21: Avoiding the problematic state of Figure 19 via reductions on error
program: ID COLON ID LPAREN ## ## Ends in an error in state: 15. ## ## program -> declaration . SEMICOLON [ # ] ## ## The known suffix of the stack is as follows: ## declaration ## ## WARNING: This example involves spurious reductions. ## This implies that, although the LR(1) items shown above provide an ## accurate view of the past (what has been recognized so far), they ## may provide an INCOMPLETE view of the future (what was expected next). ## In state 8, spurious reduction of production typ1 -> typ0 ## In state 11, spurious reduction of production declaration -> ID COLON typ1 ##
Figure 22: A problematic error state in the grammar of Figure 21, due to under-approximation
How can one work around this problem? Let us suggest three options.
One option would be to build a canonical automaton by using the --canonical switch. In this example, one would obtain a 27-state automaton, where the problem has disappeared. However, this option is rarely viable, as it duplicates many states without good reason.
A second option is to manually cause just enough duplication to remove the
problematic over-approximation. In our example, we wish to distinguish two kinds
of types and declarations, namely those that must be followed with a closing
parenthesis, and those that must be followed with a semicolon. We create
such a distinction by parameterizing typ1 and declaration with a
phantom parameter. The modified grammar is shown
in Figure 20. The phantom parameter does not affect the
language that is accepted: for instance, the nonterminal
symbols declaration(SEMICOLON) and
declaration(RPAREN) generate the same language as declaration
in the grammar of Figure 18. Yet, by giving
distinct names to these two symbols, we force the construction of an
automaton where more states are distinguished. In this example, Menhir produces
a 23-state automaton. Using --list-errors, we find that an error can be
detected in 11 of these 23 states, and by manual inspection of the
auto-generated comments, we find that for each of these 11 states, writing an
accurate diagnostic message is easy. In summary, we have selectively duplicated
just enough states so as to split the problematic error state into two
non-problematic error states.
A third and last option is to introduce an %on_error_reduce declaration
(§4.1.8) so as to prevent the detection of an error in the
problematic state 8. We see in Figure 19 that, in
state 8, the production typ1 → typ0 is ready to
be reduced. If we could force this reduction to take place, then the automaton
would move to some other state where it would be clear which
of SEMICOLON and RPAREN is expected. We
achieve this by marking typ1 as “reducible on error”.
The modified grammar is shown
in Figure 21.
For this grammar, Menhir produces a 17-state automaton.
(This is the exact same automaton as for the grammar of Figure 18,
except 2 of the 17 states have received extra reduction actions.)
Using --list-errors, we find that an error can be detected in 9 of these 17 states.
The problematic state, namely state 8, is no longer an error state!
The problem has vanished.
The third option seems by far the simplest of all, and is recommended in many situations. However, it comes with a caveat. There may now exist states whose lookahead sets are under-approximated, in a certain sense. Because of this, there is a danger of writing an incomplete diagnostic message, one that does not list all valid continuations.
To see this, let us look again at the sentence ID COLON ID LPAREN. In the grammar and automaton of Figure 18, this sentence takes us to the problematic state 8, shown in Figure 19. In the grammar and automaton of Figure 21, because more reduction actions are carried out before the error is detected, this sentence takes us to state 15, shown in Figure 22.
When writing a diagnostic message for state 15, one might be tempted to write:
“Up to this point, a declaration has been recognized. At this point, a
semicolon is expected”. Indeed, by examining the sole LR(1) item in state 15,
it looks as if SEMICOLON is the only permitted continuation. However,
this is not the case. Another valid continuation is ARROW: indeed, the
sentence
ID COLON ID ARROW ID SEMICOLON forms a valid program. In fact, if
the first token following ID COLON ID is ARROW, then in
state 8 this token is shifted, so the two reductions that take us from state 8
through state 11 to state 15 never take place. This is why, even though
ARROW does not appear in state 15 as a valid continuation, it
nevertheless is a valid continuation of ID COLON ID. The warning
produced by Menhir, shown in Figure 22, is supposed to
attract attention to this issue.
Another way to explain this issue is to point out that, by declaring
%on_error_reduce typ1, we make a choice.
When the parser reads a type and finds an invalid token, it decides that this
type is finished, even though, in reality, this type could be continued
with ARROW …. This in turn causes the parser to perform another
reduction and consider the current declaration finished, even though, in
reality, this declaration could be continued with ARROW ….
In summary, when writing a diagnostic message for state 15, one should take
into account the fact that this state can be reached via spurious reductions
and (therefore) SEMICOLON may not be the only permitted continuation.
One way of doing this, without explicitly listing all permitted continuations,
is to write: “Up to this point, a declaration has been recognized. If this
declaration is complete, then at this point, a semicolon is expected”.
The demo demos/calc-syntax-errors illustrates this approach to error
handling. It is based on the demo demos/calc, which involves a very
simple grammar of arithmetic expressions. Compared with demos/calc,
one %on_error_reduce declaration is added so as to reduce the number of error
states. There remain just 9 error states, for which we write 5 distinct syntax
error messages. These messages are stored in the file
demos/calc-syntax-errors/parserMessages.messages.
The file demos/calc-syntax-errors/dune instructs the build system to
check this file for correctness, irredundancy and completeness and to compile
this file into an OCaml module parserMessages.ml.
This OCaml module contains a single function, ParserMessages.messages,
which maps a state number to a diagnostic message. It is called from the main
module, demos/calc-syntax-errors/calc.ml.
There, we use the facilities offered by the module
MenhirLib.ErrorReports to print a full syntax error message,
which includes the precise location of the error as well as
the diagnostic message returned by
the function ParserMessages.messages.
As icing on the cake, we allow the diagnostic message to contain placeholders
of the form
$i, where i is an integer constant, understood as a 0-based
index into the parser’s stack. We replace such a placeholder with the fragment
of the source text that corresponds to this stack entry.
A number of expected-output files demonstrate the kind of syntax error
messages that we produce; see for instance
demos/calc-syntax-errors/calc03.exp and
demos/calc-syntax-errors/calc07.exp.
The CompCert verified compiler offers another real-world example. The “pre-parser” is where syntax errors are detected: see cparser/pre_parser.mly. A database of erroneous input sentences and (templates for) diagnostic messages is stored in cparser/handcrafted.messages.
As a final remark, it is worth noting that this approach to producing syntax error messages does not require using Menhir’s incremental API and table back-end. One can instead use Menhir’s code back-end with --exn-carries-state. In that case, the exception Error carries a state number, which can be used to select a syntax error message. Menhir uses this method in its own parser; see src/stage2/Driver.ml.
Menhir is able to generate a parser that whose correctness can be formally verified using the Coq proof assistant [14]. This feature is used to construct the parser of the CompCert verified compiler [18].
Setting the --coq switch on the command line enables the Coq back-end. When this switch is set, Menhir expects an input file whose name ends in .vy and generates a Coq file whose name ends in .v.
Like a .mly file, a .vy file is a grammar specification, with embedded semantic actions. The only difference is that the semantic actions in a .vy file are expressed in Coq instead of OCaml. A .vy file otherwise uses the same syntax as a .mly file. CompCert’s cparser/Parser.vy serves as an example.
Several restrictions are imposed when Menhir is used in --coq mode:
$start* and $end*
keywords (Figure 14) are not supported.
The generated file contains several modules:
Gram defines the terminal and
non-terminal symbols, the grammar, and the semantic actions.
Aut contains the automaton
generated by Menhir, together with a certificate that is checked by Coq
while establishing the soundness and completeness of the parser.
The type terminal of the terminal symbols is an inductive type, with
one constructor for each terminal symbol. A terminal symbol named Foo
in the .vy file is named Foo't in Coq. A terminal symbol per se
does not carry a the semantic value.
We also define the type token of tokens, that is, dependent pairs of a
terminal symbol and a semantic value of an appropriate type for this symbol.
We model the lexer as an object of type Streams.Stream token, that is,
an infinite stream of tokens.
The type nonterminal of the non-terminal symbols is an inductive type,
with one constructor for each non-terminal symbol. A non-terminal symbol named
Bar in the .vy file is named Bar'nt in Coq.
The proof of termination of an LR(1) parser in the case of invalid input seems
far from obvious. We did not find such a proof in the literature. In an
application such as CompCert [18], this question is not considered
crucial. For this reason, we did not formally establish the termination of the
parser. Instead, in order to satisfy Coq’s termination requirements, we use
the “fuel” technique: the parser takes an additional parameter
log_fuel of type nat such that 2log_fuel is the
maximum number of steps the parser is allowed to perform. In practice, one
can use a value of e.g., 40 or 50 to make sure the parser will never run out
of fuel in a reasonable time.
Parsing can have three different outcomes, represented by the type
parse_result.
(This definition is implicitly parameterized over the initial
state init. We omit the details here.)
Inductive parse_result :=
| Fail_pr_full: state -> token -> parse_result
| Timeout_pr: parse_result
| Parsed_pr:
symbol_semantic_type (NT (start_nt init)) ->
Stream token ->
parse_result.
The outcome Fail_pr_full means that parsing has failed because of a syntax
error. (If the completeness of the parser with respect to the grammar has been
proved, this implies that the input is invalid). It contains two pieces of information:
the state of the parser and the token which caused the error. These are provided for
error reporting, if desired. It is important to note that, even though they should be correct,
the validity of these two pieces of information is not certified by either the correctness
or the completeness theorem. For more discussion on this, see §12.1.
The outcome Timeout_pr means that the fuel has been exhausted.
Of course, this cannot happen if the parser was given an infinite amount of fuel,
as suggested above. The outcome Parsed_pr means that the parser has
succeeded in parsing a prefix of the input stream. It carries the semantic value
that has been constructed for this prefix, as well as the remainder of the input stream.
For each entry point entry of the grammar, Menhir generates a
parsing function entry, whose type is
nat -> Stream token -> parse_result.
Two theorems are provided, named entry_point_correct and
entry_point_complete. The correctness theorem states that, if a word (a
prefix of the input stream) is accepted, then this word is valid (with respect
to the grammar) and the semantic value that is constructed by the parser is
valid as well (with respect to the grammar). The completeness theorem states
that if a word (a prefix of the input stream) is valid (with respect to the
grammar), then (given sufficient fuel) it is accepted by the parser.
These results imply that the grammar is unambiguous: for every input, there is
at most one valid interpretation. This is proved by another generated theorem,
named Parser.unambiguous.
The parsers produced by Menhir’s Coq back-end must be linked with a Coq
library. This library can be installed via the command opam install coq-menhirlib.3
The Coq sources of this library can be found in
the coq-menhirlib directory of the Menhir repository.
The directory demos/coq-minicalc contains a minimal example that shows how to set things up.
The CompCert verified compiler [18,17] offers a real-world example. There, see in particular the directory cparser.
Users of the Coq mode have several options for providing error messages from the parser. If they wish, they can follow the pattern of CompCert and use Menhir’s incremental mode for a non-verified separate parser (§11.4). This may also aid in parsing languages (such as C) that need a lexical feedback loop for correct parsing.
A similar option is available in demos/calc-syntax-errors, where a second parser is used after the first to determine errors.
The parse result Fail_pr_full provides the third and simplest option.
As it carries state and token information, it allows constructing meaningful
error messages with a small amount of work. The generated function
Aut.N_of_state converts a state to a state number. While this is not as
powerful as the advanced error-handling possibilities afforded by the incremental API for
non-verified parsers, this does allow interoperability with the existing
.messages files and tooling, described in §11.1 and
§11.2. This allows error messaging without a second
parser. An example is provided in demos/coq-syntax-errors.
Note that the extra information carried by the data constructor
Fail_pr_full (and by the related data constructor Fail_sr_full
that is used internally) is not verified. This extra information is provided
for convenience, but there is no proof of its correctness.
Users who wish to ignore this extra information can use the abbreviated
notation Fail_pr and Fail_sr. This notation is used in the
statements of the theorems about the parser. It is available only in Coq code,
such as in demos/coq-minicalc, not in extracted OCaml code.
It is possible to build a variety of grammar-processing tools, also known as “grammarware” [15], on top of Menhir’s front-end. Indeed, Menhir offers a facility for dumping a .cmly file, which contains a (binary-form) representation of the grammar and automaton, as well as a library, MenhirSdk, for (programmatically) reading and exploiting a .cmly file. These facilities are described in §13.1. Furthermore, Menhir allows decorating a grammar with “attributes”, which are ignored by Menhir’s back-ends, yet are written to the .cmly file, thus can be exploited by other tools, via MenhirSdk. Attributes are described in §13.2.
The command line option --cmly causes Menhir to produce a .cmly file in addition to its normal operation. This file contains a (binary-form) representation of the grammar and automaton. This is the grammar that is obtained after the following steps have been carried out:
The library MenhirSdk offers an API for reading a .cmly file. The functor MenhirSdk.Cmly_read.Read reads such a file and produces a module whose signature is MenhirSdk.Cmly_api.GRAMMAR. This API is not explained in this document; for details, the reader is expected to follow the above links.
Attributes are decorations that can be placed in .mly files. They are ignored by Menhir’s back-ends, but are written to .cmly files, thus can be exploited by other tools, via MenhirSdk.
An attribute consists of a label and a payload. An attribute label is an OCaml identifier, such as cost, or a list of OCaml identifiers, separated
with dots, such as my.label. An attribute payload is an OCaml expression of arbitrary type, such as 1 or "&&" or print_int.
(The payload is not parsed or type-checked, but must be well-formed according
to OCaml’s lexical conventions: that is, inside it, braces, parentheses,
single and double quotes, and comment delimiters must be balanced.)
Following the syntax of OCaml’s attributes, an attribute’s label and payload
are separated with one or more spaces, and are delimited by [@ and
]. Thus,
[@name foo]
and
[@cost 1]
and
[@printer print_int]
are examples of attributes.
An attribute can be attached at one of five levels:
% sign and must appear
in the declarations section (§4.1). For example, the following
is a valid declaration:
%[@trace true]
INT:
%token<int> INT [@cost 0] [@printer print_int]
expr:
expr [@default EConst 0]:
i = INT { EConst i }
| e1 = expr PLUS e2 = expr { EAdd (e1, e2) }
An attribute can be attached with a parameterized nonterminal symbol:
option [@default None] (X):
{ None }
| x = X { Some x }
An attribute cannot be attached with a nonterminal symbol that is
decorated with the %inline keyword.expr*:
exprs:
LPAREN es = expr* [@list true] RPAREN { es }
option(X):
{ None } [@name none]
| x = X
{ Some x } [@name some]
If a nonterminal symbol is marked %inline then it cannot carry an attribute, and a use of it cannot carry an attribute.
As a convenience, it is possible to attach many attributes with many (terminal
and nonterminal) symbols in one go, via an %attribute declaration, which must
be placed in the declarations section (§4.1).
For instance, the following declaration attaches both of the attributes
[@cost 0] and [@precious false]
with each of the symbols
INT and id:
%attribute INT id [@cost 0] [@precious false]
An %attribute declaration can be considered syntactic sugar: it is desugared away in terms of the five forms of attributes presented earlier (§13.2.2). The command line switch --only-preprocess can be used to see how it is desugared.
If an attribute is attached with a parameterized nonterminal symbol, then,
when this symbol is expanded away (§5.2),
the attribute is transmitted to every
instance. For instance, in an earlier example, the attribute
[@default None] was attached with the parameterized symbol
option. Then, every instance of option, such as
option(expr), option(COMMA), and so on, inherits this
attribute. To attach an attribute with one specific
instance only, one can use an %attribute declaration. For instance,
the declaration %attribute option(expr) [@cost 10] attaches
an attribute with the nonterminal symbol option(expr), but
not with the symbol option(COMMA).
If an attribute is attached with a production for a parameterized nonterminal symbol, then, when this symbol is expanded away (§5.2), this attribute is transmitted to every instance of this production.
As an exception to this general rule, @name attributes receive
special treatment: their payload is specialized. For instance, assuming that
the parameterized symbol option(X) is defined as follows:
option(X):
{ None } [@name none]
| x = X
{ Some x } [@name some]
then instantiating the parameter X with expr results in the
following definition:
option(expr):
{ None } [@name none_expr]
| x = expr
{ Some x } [@name some_expr]
The payload of each @name attribute has been extended with
an underscore character _ followed with the actual
parameter expr.
(If the actual parameter contains parentheses or commas,
they are replaced with underscore characters.)
This special behavior is intended to allow each production
to receive a unique name.
When a production whose left-hand side is marked %inline (the callee) is inlined (§5.3) into another production (the caller), the attributes of the caller are transmitted to the new production, while the attributes of the callee are lost. (This policy may change in the future.)
As an exception to this general rule,
@name attributes receive special treatment:
the @name attributes of the callee and caller are combined, as follows.
If the caller and the callee both carry a @name attribute,
then the attribute payloads are concatenated,
and an underscore character _ is
inserted between them.
If only the caller or only the callee carries a @name attribute,
then this attribute is preserved.
For example, after inlining, the following definitions:
expr:
| e1 = expr; op = binop; e2 = expr
{ EBinOp (e1, op, e2) } [@name binop]
%inline binop:
| ADD { BAdd } [@name add]
| SUB { BSub } [@name sub]
give rise to the following result:
expr:
| e1 = expr; op = ADD; e2 = expr
{ let op = BAdd in EBinOp (e1, op, e2) }
[@name binop_add]
| e1 = expr; op = SUB; e2 = expr
{ let op = BSub in EBinOp (e1, op, e2) }
[@name binop_sub]
This special behavior is intended to allow each production to receive a unique name.
This section explains some details of the compilation workflow, including OCaml type inference and its repercussions on dependency analysis (§14.1) and compilation flags (§14.2). This material should be of interest only to authors of build systems who wish to build support for Menhir into their system. Ordinary users should skip this section and use a build system that knows about Menhir, such as dune (preferred; §16) or ocamlbuild.
In an ideal world, the semantic actions in a .mly file should be well-typed according to the OCaml type discipline, and their types should be known to Menhir, which may need this knowledge. (When --inspection is set, Menhir needs to know the OCaml type of every nonterminal symbol.) To address this problem, three approaches exist:
dune follows the third approach behind the scenes.
The simplest thing to do is to run Menhir without any of the flags described in the following (§14.1.2, §14.1.3). Then, the semantic actions are not type-checked, and their OCaml type is not inferred. (This is analogous to using ocamlyacc.) The drawbacks of this approach are as follows:
The second approach is to let Menhir invoke the OCaml compiler so as to type-check the semantic actions and infer their types. This is done by invoking Menhir with the --infer switch, as follows.
--infer. This switch causes the semantic actions to be checked for
type consistency before the parser is generated. To do so, Menhir generates a mock .ml file, which contains just the semantic actions, and
invokes the OCaml compiler, under the form ocamlc -i, so as to
type-check this file and infer the types of the semantic actions. Menhir then
reads this information and produces real .ml and .mli files.
--ocamlc command. This switch controls how ocamlc is invoked. It allows setting both the name of the executable and the command line options that are passed to it.
One difficulty with this approach is that the OCaml compiler usually needs to consult a few .cm[iox] files. Indeed, if the .mly file contains a reference to an external OCaml module, say A, then the OCaml compiler typically needs to read one or more files named A.cm[iox].
This implies that these files must have been created first. But how is one supposed to know, exactly, which files should be created first? One must scan the .mly file so as to find out which external modules it depends upon. In other words, a dependency analysis is required. This analysis can be carried out by invoking Menhir with the --depend switch, as follows.
--depend. This switch causes Menhir to generate dependency information for use in conjunction with make. When invoked in this mode, Menhir does not generate a parser. Instead, it examines the grammar specification and prints a list of prerequisites for the targets basename.cm[iox], basename.ml, and basename.mli. This list is intended to be textually included within a Makefile. To produce this list, Menhir generates a mock .ml file, which contains just the semantic actions, invokes ocamldep, and postprocesses its output.
--raw-depend. This switch is analogous to --depend. However, in this case, ocamldep’s output is not postprocessed by Menhir: it is echoed without change. This switch is not suitable for direct use with make ; it is intended for use with omake or ocamlbuild, which perform their own postprocessing.
--ocamldep command. This switch controls how ocamldep is invoked. It allows setting both the name of the executable and the command line options that are passed to it.
The third approach is to let Menhir request and receive OCaml type information without allowing Menhir to invoke the OCaml compiler. There is nothing magic about this: to achieve this, Menhir must be invoked twice, and the OCaml compiler must be invoked (by the user, or by the build system) in between. This is done as follows.
--infer-write-query mockfilename. When invoked in this mode, Menhir does not generate a parser. Instead, generates a mock .ml file, named mockfilename, which contains just the semantic actions. Then, it stops.
It is then up to the user (or to the build system) to invoke ocamlc -i
so as to type-check the mock .ml file and infer its signature. The output of
this command should be redirected to some file sigfilename. Then, Menhir can be invoked again, as follows.
--infer-read-reply sigfilename. When invoked in this mode, Menhir assumes that the file sigfilename contains the result of running
ocamlc -i on the file mockfilename. It reads and parses this file,
so as to obtain the OCaml type of every semantic action, then proceeds
normally to generate a parser.
This protocol was introduced on 2018/05/23; earlier versions of Menhir do not support it. Its existence can be tested as follows:
--infer-protocol-supported. When invoked with this switch, Menhir immediately terminates with exit code 0. An earlier version of Menhir, which does not support this protocol, would display a help message and terminate with a nonzero exit code.
The following switches allow querying Menhir so as to find out which compilation flags should be passed to the OCaml compiler and linker.
--suggest-comp-flags. This switch causes Menhir to print a set of suggested compilation flags, and exit. These flags are intended to be passed to the OCaml compilers (ocamlc or ocamlopt) when compiling and linking the parser generated by Menhir. What flags are suggested? In the absence of the --table switch, no flags are suggested. When --table is set, a -I flag is suggested, so as to ensure that MenhirLib is visible to the OCaml compiler.
--suggest-link-flags-byte. This switch causes Menhir to print a set of suggested link flags, and exit. These flags are intended to be passed to ocamlc when producing a bytecode executable. What flags are suggested? In the absence of the --table switch, no flags are suggested. When --table is set, the object file menhirLib.cma is suggested, so as to ensure that MenhirLib is linked in.
--suggest-link-flags-opt. This switch causes Menhir to print a set of suggested link flags, and exit. These flags are intended to be passed to ocamlopt when producing a native code executable. What flags are suggested? In the absence of the --table switch, no flags are suggested. When --table is set, the object file menhirLib.cmxa is suggested, so as to ensure that MenhirLib is linked in.
--suggest-menhirLib. This switch causes Menhir to print (the absolute path of) the directory where MenhirLib was installed.
--suggest-ocamlfind. This switch is deprecated and may be removed in the future. It always prints false.
Roughly speaking, Menhir is 90% compatible with ocamlyacc. Legacy ocamlyacc grammar specifications are accepted and compiled by Menhir. The resulting parsers run and produce correct parse trees. However, parsers that explicitly invoke functions in the module Parsing behave slightly incorrectly. For instance, the functions that provide access to positions return a dummy position when invoked by a Menhir parser. Porting a grammar specification from ocamlyacc to Menhir requires replacing all calls to Parsing with new Menhir-specific keywords (§7).
Here is an incomplete list of the differences between ocamlyacc and Menhir. The list is roughly sorted by decreasing order of importance.
$1,
$2, and so on. Menhir allows semantic values to be explicitly named.raise Parse_error within
semantic actions are deprecated. The function parse_error is
deprecated. They are replaced with keywords (§10).⋄ Is Menhir faster than ocamlyacc? What is the speed difference between menhir and menhir --table? A (not quite scientific) benchmark suggests that the parsers produced by ocamlyacc and menhir --table have comparable speed, whereas those produced by menhir are between 2 and 5 times faster. This benchmark excludes the time spent in the lexer and in the semantic actions.
⋄ How do I write Makefile rules for Menhir? This can be a bit tricky. If you must do this, see §14. It is recommended instead to use a build system with built-in support for Menhir, such as dune (preferred) or ocamlbuild.
⋄ How do I use Menhir with ocamlbuild?
Pass -use-menhir to ocamlbuild.
To pass options to Menhir,
pass -menhir "menhir <options>" to ocamlbuild.
To use Menhir’s table back-end,
pass -menhir "menhir --table" to ocamlbuild,
and either
pass -package menhirLib to ocamlbuild or add the tag package(menhirLib) in the _tags file.
To combine multiple .mly files,
say a.mly and b.mly,
into a single parser,
say parser.{ml,mli},
create a file named parser.mlypack
that contains the module names A B.
See the directory demos/ocamlbuild for examples.
To deal with .messages files (§11),
use the rules provided in the file demos/ocamlbuild/myocamlbuild.ml.
⋄ How do I use Menhir with dune? Please use dune version 1.4.0 or newer, as it has appropriate built-in rules for Menhir parsers. In the simplest scenario, where the parser resides in a single source file parser.mly, the dune file should contain a “stanza” along the following lines:
(menhir (modules parser) (flags --explain --dump) (infer true) )
Ordinary command line switches, like --explain and --dump, are passed as part of the flags line, as done above. The --infer switch has special status and should not be used directly; instead, write (infer true) or (infer false), as done above. (The default is true.) The --table switch can also be listed as part of the flags line; if you do so, then you must add menhirLib to the list of libraries that your code requires, as in the following example:
(executable (name myexecutable) (libraries menhirLib) )
If the flags --table and --unparsing switch are listed as part of the flags line, then the libraries menhirLib and menhirCST is required.
The directory demos offers several examples. For more details, see dune’s documentation. To deal with .messages files (§11), please use and adapt the rules found in the file src/stage2/dune.
⋄ My .mly file begins with a module alias declaration module F
= Foo. Because of this, the .mli file generated by Menhir contains
references to F instead of Foo. This does not make sense!
Beginning with Menhir 20200525, Menhir prefers to use the types inferred by
the OCaml compiler over the types provided by the user in %type declarations. (This may sound strange, but these types can differ in some
situations that involve polymorphic variants. Using the inferred type is
required for type soundness.)
In the presence of a module alias declaration such as module F =
Foo, OCaml can infer types that begin with F. instead of
Foo., and Menhir does not detect that F is a local
name.
The fix is to place the module alias declaration
inside open struct ... end (§4.1.1).
⋄ Menhir reports more shift/reduce conflicts than ocamlyacc! How come? ocamlyacc sometimes merges two states of the automaton that Menhir considers distinct. This happens when the grammar is not LALR(1). If these two states happen to contain a shift/reduce conflict, then Menhir reports two conflicts, while ocamlyacc only reports one. Of course, the two conflicts are very similar, so fixing one will usually fix the other as well.
⋄ I do not use ocamllex. Is there an API that does not involve lexing
buffers? Like ocamlyacc, Menhir produces parsers whose monolithic API
(§9.1) is intended for use with ocamllex. However, it is
possible to convert them, after the fact, to a simpler, revised API. In the
revised API, there are no lexing buffers, and a lexer is just a function from
unit to tokens. Converters are provided by the library module
MenhirLib.Convert. This can be useful, for instance, for users of
sedlex, the Unicode-friendly lexer generator. Also, please note that Menhir’s
incremental API (§9.2) does not mention the type
Lexing.lexbuf. In this API, the parser expects to be supplied with
triples of a token and start/end positions of type Lexing.position.
⋄ Is there other useful magic in MenhirLib? There is some. The module MenhirLib.ErrorReports offers some facilities for constructing syntax error messages. The module MenhirLib.LexerUtil offers facilities for extracting the position of a syntax error out of the lexing buffer and displaying it in a readable way.
⋄ I need both %inline and non-%inline versions of a non-terminal symbol. Is this possible? Define an %inline version first, then use it to define a non-%inline version, like this:
%inline ioption(X): (* nothing *) { None } | x = X { Some x }
option(X): o = ioption(X) { o }
This can work even in the presence of recursion, as illustrated by the following definition of (reversed, left-recursive, possibly empty) lists:
%inline irevlist(X): (* nothing *) { [] } | xs = revlist(X) x = X { x :: xs }
revlist(X): xs = irevlist(X) { xs }
The definition of irevlist is expanded into the definition of revlist,
so in the end, revlist receives its normal, recursive definition. One can
then view irevlist as a variant of revlist that is inlined one level
deep.
⋄ Can I ship a generated parser while avoiding a dependency on MenhirLib?
Yes. One option is to use the code back-end (that is, to not
use --table). In this case, the generated parser is self-contained. Another
option is to use the table back-end (that is, use --table) and include a
copy of the files menhirLib.{ml,mli} together with the generated
parser. The command menhir --suggest-menhirLib will tell you where to
find these source files.
⋄ Why is $startpos off towards the left? It seems to include
some leading whitespace. Indeed, as of 2015/11/04, the computation of
positions has changed so as to match ocamlyacc’s behavior. As a result,
$startpos can now appear to be too far off to the left. This is
explained in §7. A solution may be to use
$symbolstartpos instead.
⋄ Can I pretty-print a grammar in ASCII, HTML, or LATEX format? Yes. Have a look at obelisk [5].
⋄ Does Menhir support mid-rule actions? Yes. See midrule and its explanation in §5.4.
After experimenting with Knuth’s canonical LR(1) technique [16], we found that it really is not practical, even on today’s computers. For this reason, Menhir implements a slightly modified version of Pager’s algorithm [20], which merges states on the fly if it can be proved that no reduce/reduce conflicts will arise as a consequence of this decision. This is how Menhir avoids the so-called mysterious conflicts created by LALR(1) parser generators [8, section 5.7].
Menhir’s algorithm for explaining conflicts is inspired by DeRemer and Pennello’s [7] and adapted for use with Pager’s construction technique.
By default, Menhir produces code, as opposed to tables. This approach has been explored before [3,10]. Menhir performs some static analysis of the automaton in order to produce more compact code.
When asked to produce tables, Menhir performs compression via first-fit row displacement, as described by Tarjan and Yao [25]. Double displacement is not used. The action table is made sparse by factoring out an error matrix, as suggested by Dencker, Dürre, and Heuft [6].
The type-theoretic tricks that triggered our interest in LR parsers [23] are implemented in Menhir’s code back-end. (It took 16 years, from the initial idea in 2005 to the re-implementation of the code back-end in 2021.) A generalized algebraic data type (GADT) is used to describe the shape of the stack and the relationship that exists between the shape of the stack and the current state of the automaton.
The main ideas behind the Coq back-end are described in a paper by Jourdan, Pottier and Leroy [14]. The C11 parser in the CompCert compiler [18] is constructed by Menhir and verified by Coq, following this technique. How to construct a correct C11 parser using Menhir is described by Jourdan and Pottier [13].
The approach to error reports presented in §11 was proposed by Jeffery [11] and further explored by Pottier [21] and by Bour and Pottier [4].
The unparsing API and the settlement algorithm were proposed by Pottier [22].
This document was translated from LATEX by HEVEA.